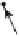Graphics Reference
In-Depth Information
Figure 3.15.
A geometric explanation of
the transformation defined by
(3.30).
z
Q(x,y,ax+by)
z = by
X
z = ax
ax + by - z = 0
y
P(x,y,0)
x
P¢(x/(ax+by+1),y/(ax+by+1,0)
-1
manner for
R
n
, but restricting ourselves to
R
n
would lead to the same shortcomings
that we saw for
R
2
. The proper setting for all these maps is again projective space.
N-dimensional projective space
P
n
was defined in Section 3.4. This section briefly
describes how the definitions and results of the last few sections extend.
First of all, in analogy with
P
2
, one can think of
P
n
as the set of lines through the
origin in
R
n+1
. Furthermore, there is again a natural imbedding of
R
n
into
P
n
.
Definition.
The map
n
n
i :
RP
Æ
defined by
(
)
=
[
]
i xx
,
,...,
x
xx
,
,...,
x
,
1
12
n
12
n
is called the
standard imbedding of
R
n
in
P
n
.
Identifying a point
p
of Euclidean space with its image i(
p
) in projective space
allows us to consider
R
n
as a subset of
P
n
. We shall do so from now on and consider i as
an inclusion map. Also, by identifying [x
1
,x
2
,..., x
i
,x
i + 1
] in
P
i
with [x
1
,x
2
,..., x
i
,0,x
i+1
] in
P
i+1
, we get
natural inclusions
P
i
Ã
P
i+1
and a commutative diagram
0
1
2
n
-
1
n
PPP
ÃÃÃÃ
...
P
Ã
P
||
»»
»
»
0
1
2
n
-
1
n
RRR
ÃÃ ÃÃ
...
R
Ã
R
.
The points of
P
n
-
R
n
Definition.
are called
ideal points
. All the other points are
called
real points
.
The ideal points in
P
n
are the points of the form [x
1
,..., x
n
, 0]. They can also be
thought of as corresponding to families of parallel lines in
R
n
. Lines, planes, etc., in
P
n
are defined in terms of solutions to appropriate sets of homogeneous equations.