Graphics Reference
In-Depth Information
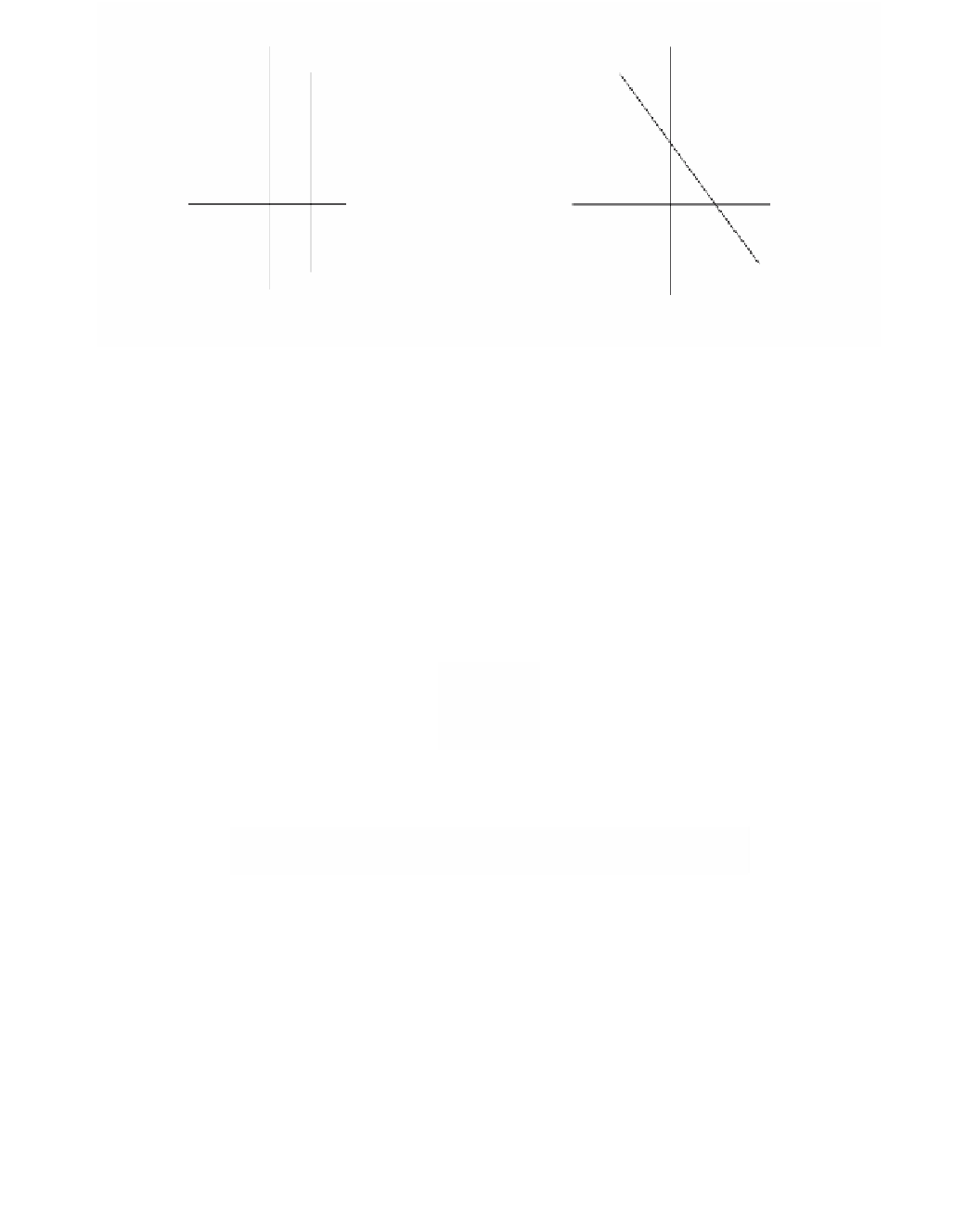
y
y¢
x = c
1/a
x
x¢
c
c
(a)
(b)
Figure 3.14.
A vanishing point.
sect in (0,1/a). See Figure 3.14. The point (0,1/a) is called a
vanishing point
. The reader
should recall the discussion of vanishing points in Section 3.2.
The last observation about the map U
a
is that it is a well-defined map on all of
projective space even though the affine central projection with center (0,-1/a) is not,
since it is not defined for the points on the line y =-1/a. The simple-minded expla-
nation for this discrepancy is that affine central projections involve a division, so that
one has to worry about zero denominators, whereas the associated projective trans-
formations do not.
Finally, consider the projective transformation U
a,b
:
P
2
Æ
P
2
defined by the matrix
10
01
001
a
b
Ê
ˆ
Á
Á
˜
˜
.
(3.30)
Ë
¯
The affine map T that it induces also has a simple geometric description. Let T
1
be
the parallel projection in direction
e
3
of the x-y plane onto the plane
X
defined by
ax
+-=0.
by
z
Let T
2
be the perspectivity with center (0,0,-1) from
X
back to the x-y plane. It is easy
to show that T = T
2
T
1
. See Figure 3.15. The point
P
in the figure gets mapped to
Q
in
the plane
X
by T
1
and then to
P
¢ by T
2
.
3.5
Beyond the Plane
Central projections, perspectivities, projective transformations, fractional transfor-
mations, and homogeneous coordinates can all be defined in a straight forward