Graphics Reference
In-Depth Information
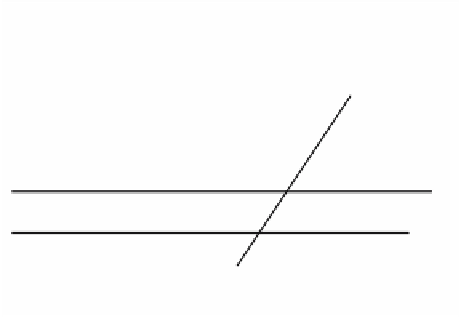
Figure 3.7.
The view of three railroad
ties determines the rest.
z
eye
y
D¢
C¢
B¢
A¢
12
·····
n
x
AB
D
view
plane
constraints, but from then on the relative spacing of the remaining ties or rungs in
the view is fixed. See Figure 3.7.
Returning to our analysis of parallel and central projections, the next definition
is the best we can do in the context of affine geometry.
Definition.
A
projective transformation
or
projectivity
of a plane
X
to itself is a “map”
T such that
(a) The domain of T is either
X
or
X
minus a line
L
. The range of T is either
X
or
X
minus a line
L
¢.
(b) T is one-to-one.
(c) T preserves collinearity when defined.
(d) T preserves the cross-ratio when defined.
3.2.3. Theorem.
A projective transformation has the following properties:
(1) Ordinary lines go to ordinary lines.
(2) The map sets up a natural one-to-one correspondence between lines.
(3) A family of concurrent lines goes into a family of concurrent lines or a family
of parallel lines.
(4) A family of parallel lines goes into a family of parallel lines or a family of con-
current lines.
(5) Conics go to conics. More precisely, any nondegenerate conic may be mapped
onto any other nondegenerate conic by a projective transformation.
Proof.
See [Gans69]. Theorem 3.2.3 can be proved directly or deduced from
Theorem 3.2.5 below.
3.2.4. Theorem.
There is a unique projective transformation in which a given line
L
has no image and which sends given noncollinear points
A
,
B
, and
C
into given
noncollinear points
A
¢,
B
¢, and
C
¢, respectively.
Proof.
See [Gans69].