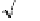Graphics Reference
In-Depth Information
substituting into the equation for
X
gives that
3
2
2
13
3
13
3
13
2
13
È
Í
˘
˙
++-
È
Í
˘
˙
=
x
+
z
3
y
x
+
z
0
,
that is,
13
2
313
y
+
z
=
0
,
is the equation for
X
1
. This shows that
X
1
contains the x-axis and is orthogonal to the
y-z plane, justifying our construction. This finishes Example 2.5.1.4.
2.5.2
Frames Revisited
The last section described what might be called the geometric approach to defining
motions in
R
3
. Some of the computations got rather complicated. The power of frames
comes from their ability to define a motion M in terms of an orthonormal basis, which
is typically easier to define than the rotations and reflections that might describe M
if we were to use the approach from the last section. We saw some of this in Section
2.2.8, but it is especially going to pay off here. As our first example we redo Example
2.5.1.4.
2.5.2.1. Example.
To find the rotation R that rotates the plane
X
defined by
3
2
xyz
++=
3
0
to the x-y plane.
Solution.
We use the same notation as in Example 2.5.1.4. See Figure 2.29. Apply-
ing the Gram-Schmidt algorithm to the basis
A
(2,0,-3) and
B
(0,1,-3) for
X
gives us
an orthonormal basis
1
13
1
713
(
)
(
)
u
=
20 3
,,
-
,
and
u
=
-
18 13
, ,
-
12
.
1
2
The equation for
X
tells us that
n
= (3/2,3,1) is a normal vector for the plane. Let
n
n
1
7
==
(
)
u
362
,, ,
3