Information Technology Reference
In-Depth Information
F
E
F
E
A
=
A
E
C
C
(b)
Γ
B ⊗ C
D
C
E ⊗ F
(a)
(c)
Fig. 3.
Γ
(a), constraint graph for CSA
Γ
;
A ⊗ B ⊗ C F
(b), and constraint graph
for CSA
Γ
;
A ⊗ C F ⊗ E
2
(c).
3.2
Removing Redundant CSCs
After the possibly required literals have been determined, we can throw away all
CSCs, which include at least one literal which is not included in the constraint
graph. In that way the search space would be pruned and search made more
ecient. Provability of a particular CSA would not be affected by removing
these CSCs.
Theorem 2.
Given a CSA and a set of edges
D
e
of the constraint graph
,
which was constructed for the CSA, we can discard all CSCs
c ∈ Γ
,which
satisfy condition
D
∃l.
((
l ∈
∨ l ∈
∧ l ∈ D
e
∧
≡∅
succ
(
c
)
ant
(
c
))
succ
(
c
)
)
without
affecting the provability of the CSA.
Proof.
If there is a CSC
c ∈ Γ
of a CSA such that
∃l.
((
l ∈
∨ l ∈
ant
(
c
)
succ
(
c
))
∧ l ∈ D
e
), then it means that
c
was not considered during construction
of constraint graph
. Therefore
c
is not considered relevant for finding a proof
for the particular CSA and can be discarded.
D
CSC reduction is illustrated in Fig. 3(c), where a constraint graph is gen-
erated for CSA
Γ
;
A ⊗ C F ⊗ E
2
. Since literals
B
and
D
are not present in
the constraint graph, they are considered irrelevant for PD. Therefore all CSCs
c
such that
B ∈
succ
(
c
)canbe
removed without affecting the provability result of the original problem. Hence
ant
(
c
)or
D ∈
ant
(
c
)or
B ∈
succ
(
c
)or
D ∈
B
⊗
C
D
can be removed from
Γ
.
3.3 The Computational Complexity
of Constructing Abstraction Hierarchies
According to [7] the complexity of building the constraint graph is
O
(
n
l
),
where
n
is the number of different literals in a CSC,
o
is the maximum number
of CSCs relevant for achieving any given literal, and
l
is the total number of
different literals in succedents of relevant CSCs. Building a hierarchy is also
O
(
n
∗
o
∗
l
) since the number of edges in the graph is bounded by
n ∗ o ∗ l
and
the complexity of the graph algorithms used is linear.
∗
o
∗
4
PD with Abstraction Hierarchies
To prove hierarchically, sequents are first mapped to the highest level of ab-
straction. This is done by substituting literals, not essential at that abstraction

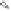



Search WWH ::

Custom Search