Cryptography Reference
In-Depth Information
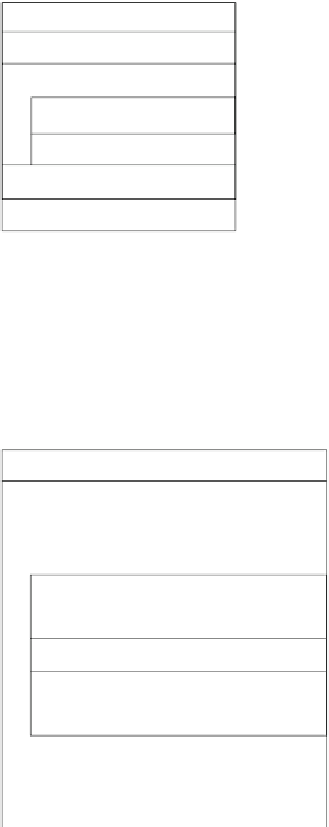
Lokatorpolynom nach EUKLID
Grundlage dieser Berechnung bildet der EUKLIDische Algorithmus zur Be-
stimmung des größten gemeinsamen Teilers (ggT). Im Folgenden soll kurz die
Entwicklung vom ggT zum Lokatorpolynom aufgezeigt werden. Zunächst die
Berechnung des ggT
(
a, b
)
zweier natürlicher Zahlen
a
und
b
mit
a>b
:
a
;
b
r
−
1
:=
a
;
r
0
:=
b
;
i
:= 0
r
i
=0
i
:=
i
+1
r
i
:=
r
i−
2
r
i−
1
(
a, b
):=
r
i−
1
(
a, b
)
Der Vorteil der fortgesetzten Restbildung liegt in der schnellen Konvergenz.
Der unten stehende erweiterte EUKLIDische Algorithmus berechnet darüber
hinaus einen Zusammenhang für jeden Rest
r
i
in Abhängigkeit von
a
und
b
mit
r
i
=
b
·
w
i
+
a
·
v
i
und das multiplikativ Inverse
b
−
1
mod
a
, vorausgesetzt,
a
und
b
sind teilerfremd. Das multiplikativ Inverse ist beispielsweise für die
Schlüsselgenierung bei der Anwendung des RSA-Verfahrens (ein asymmetri-
sches Kryptoverfahren) von Bedeutung.
a
;
b
r
−
1
:=
a
;
r
0
:=
b
;
i
:= 0
w
−
1
:= 0;
w
0
:= 1;
v
−
1
:= 1;
v
0
:= 0
r
i
=0
i
:=
i
+1
r
i
:=
r
i−
2
r
i−
1
q
:=
r
i−
2
r
i−
1
w
i
:=
w
i−
2
− q · w
i−
1
v
i
:=
v
i−
2
− q · v
i−
1
(
a, b
):=
r
i−
1
r
i−
1
:=
b · w
i−
1
+
a · v
i−
1
b
−
1
:=
w
i−
1
a,
(
a, b
)=1
(
a, b
)
Hinweis
:
a
mod
b
stellt den Rest bei der Division von
a
durch
b
dar,
a
div
b
berechnet den ganzzahligen Teil der Division.