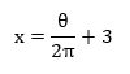RENDERING - User Interface Programming for Games - page 112

The first step will be to calculate the number of vertices we will need, for the base of the
cone we use a circle cut up into pieces by the angle Ɵ, from this we can determine that the
number of vertices x will be:
Weneedthreeadditionalvertices,onewillbetheorigin,setatthecenterofthecirclewhich
we will use to cap the cone, the other one is the top vertex, and the last one is used to du-
plicate the closing vertex. Without this duplicated vertex the texture coordinates would not
be correct and the texture mapping would have artifacts.
Setting the origin and top vertices is trivial and we can do it right away.
const int numVertices = (360 / degrees) + 3;
vertex_default vertices[numVertices];
vertices[0] = vertex_default(math::vector3::UnitY, color::WHITE, math::vector2(0.5f, 1.f));
vertices[numVertices - 1] = vertex_default(-math::vector3::UnitY, color::WHITE, math::vector2(0.5f, 0.f));
Notice in this case we opt for working in degrees, it provides a more straightforward input
parameter for users and it also simplifies using loops as we avoid doing floating point cal-
culations at the cost of some precision.
The next step is to calculate the vertices of the cone's circle, we iterate over a full circle in
increments of Ɵ, and we calculate the x,z coordinates, the y coordinate will remain fixed at
-1, which is where we set the origin.
for ( int i = 0, j = 1; i <= 360; i += degrees, ++j )
{
const float theta = math::DegreesToRadians(i);
const float x = sinf(theta);
const float z = cosf(theta);
vertices[j] = vertex_default(math::vector3(x, -1.f, z), color::WHITE, math::vector2((j % 2) == 0 ? 0.f : 1.f, 0.f));
}
We now have all the vertices that will make up the cone, the next step is to calculate the
indices for the triangles that will make up the sides of the cone as well as the cap.
Thenumberofindiceswillbethreetimesthenumberofverticesforthesidesplusthethree
time the number of vertices for the cap (the cap has the same amount of faces as the sides).
unsigned short indices[2 * (numVertices * 3)];