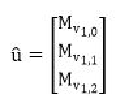Game Development Reference
In-Depth Information
form the alignment of the quad at the moment we draw it, it is at this point in which we
will have the most up to date view matrix, which we need to compute the direction vector
to the camera.
The camera's view matrix is used to transform vertices from world-space into view-space,
it holds the rotation and translation magnitudes by which vertices are transformed to be
represented in view space. The inverse view matrix represents the camera's transformation
matrix, this is the world-space matrix of the camera's orientation and position in the world.
Given the view matrix:
Wewillneedtocalculatetheinverseviewmatrix,whichwewillusetoextractthecamera's
world space position
p
from.
With the camera's world space position we can now calculate the direction vector from the
quad's world space position
q
to the camera's
p
.
Thedirectionvector
v
isalsothequad'snormalvector,given
thenormalvector
v
wecanconstruct
the orthonormal basis by computing the cross product of the normal vector with the cam-
era view's up vector, this will give us a perpendicular vector we will call the right vector.
We then use the
up
vector to compute the
right
.