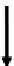Civil Engineering Reference
In-Depth Information
V
P
x
Vt
L
y
FIGURE 4.6
Moving concentrated load on a simple beam.
where
δ
(
ξ
)
is the Dirac delta function, which mathematically describes a constant
velocity unit concentrated force at
ξ =
x
−
Vt
, considering the force
p(x
,
t)
as a
unit impul
se
force (Tse et al., 1978);
P
is the concentrated force and is equal to
F
−
m
v
(
d
2
y(Vt
,
t)/
d
t
2
)
(d'Alembert's principle of inertial effects);
F
=
F(t)
+
m
v
g
,
where
F(t)
is the dynamic forces from concentrated moving load, such as forces from
locomotive suspension system dynamics,
m
v
is the mass of the concentrated force,
and
g
is the acceleration due to gravity.
For simply supported boundary conditions with initial conditions of zero displace-
ment and velocity, Equation 4.4, for a moving constant concentrated force, can be
written as
EI
∂
4
y(x
,
t)
∂x
4
m
∂
2
y(x
,
t)
∂t
2
c
∂y(x
,
t)
∂t
+
+
= δ
(
ξ
)P
.
(4.11)
For bridges carrying freight rail traffic, we can assume a relatively slow vehi-
cle speed,
V
, and neglect
th
e dynamic vehicle suspension load,
F(t)
=
0, which
(
d
2
y(Vt
,
t)/
d
t
2
)
means that
P
1 [since for simply
supported spans it is generally sufficient to consider only the fundamental mode of
vibration (Veletsos and Huang, 1970)], the solution of Equation 4.11 may be achieved
by transformation techniques as (Fryba, 1996)
=
m
v
[
g
−
]
. In this case, using
i
=
∞
2
FL
3
π
1
y(x
,
t)
=
i
2
i
2
(i
2
ω
1
)
2
4
EI
ω
1
)
2
)
2
ω
1
)
2
(
−
(
ω
/
+
4
(
ω
/
ω
c
/
i
=
1
ω
1
)
i
2
(i
2
ω
1
)
2
⎡
⎣
⎤
⎦
ω
1
)
2
)
i
2
i
2
ω
1
)
2
sin
i
i(
ω
/
−
(
ω
/
−
2
(
ω
c
/
−
(
ω
/
ω
t
−
i
4
−
(
ω
c
/
ω
1
)
2
π
e
−ω
c
t
sin
ω
1
)
cos
i
sin
i
x
L
,
2
e
−ω
c
t
ω
i
− ω
c
t
−
ω
ω
1
)(
ω
c
/
ω
−
2
i(
/
t
cos
c
t
2
×
ω
i
− ω
(4.12a)
where
F
=
m
v
g
[when
F(t)
=
0],
ω =
(
π
V/L)
(forcing frequency of
p
(xt)
),
and
ω
1
is the first or fundamental frequency of span (resonance occurs when
ω = ω
1
).