Civil Engineering Reference
In-Depth Information
V
w
(
x
-
Vt, t
)
x
Vt
L
y
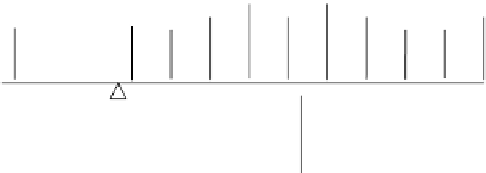
FIGURE 4.5
Moving continuous load on a simple beam.
(withrespecttothehorizontalaxis),
m
isthemassofthesuperstructureperunitlength,
c
is the equivalent coefficient of viscous damping of the superstructure and is equal
to 2
m
ω
c
is the viscous damping frequency, and
p(x
,
t)
is the dynamic load on the
bridge at distance
x
and time
t
.
Mass develops inertial forces in direct proportion, and in opposite direction, to its
acceleration in accordance with d'Alembert's principle. These inertial forces must be
included in the analysis of relatively light steel railway bridges
∗
traversed by large
locomotive and train weights.
For a moving continuous load (Figure 4.5), the load on the bridge may be
expressed as
ω
c
,
)
d
2
y(x
,
t)
d
t
2
p(x
,
t)
=
w(
ξ
,
t)
−
m
w
(
ξ
,
(4.5)
where
w(
Vt
and time
t
;
m
w
(
ξ
)
=
w(
ξ
,
t)
/
g
is the mass of uniform load at distance
ξ =
x
−
Vt
and time
t
;
V
=
is the constant velocity of load; and
g
is the acceleration due to gravity.
Since, due to the inertial effects of the st
a
tionary continuous mass, the load,
p(x
,
t)
, depends on the superstructure response,
y(x
,
t)
, it is necessary to determine the
derivative expression in Equation 4.5. The derivative, at
ξ
,
t)
is the magnitude of uniform load at distance
ξ =
x
−
ξ =
0(
x
=
Vt
) with constant
train velocity,
V
, can be expanded as (Fryba, 1996)
d
2
y(Vt
,
t)
d
t
2
V
2
∂
2
y(Vt
,
t)
∂x
2
2
V
∂
2
y(Vt
,
t)
∂
2
y(Vt
,
t)
∂t
2
=
+
∂x∂t
+
.
(4.6)
ξ
=
w
, simply supported boundary
conditions(commonforsteelrailwaybridges),initialconditionsofzerodisplacement,
and velocity, Equation 4.4 (with Equations 4.5 and 4.6) can be written as
For a uniform continuous moving load,
w(
,
t)
EI
∂
4
y(x
,
t)
∂x
4
m
w
V
2
∂
2
y(x
,
t)
m
w
)
∂
2
y(x
,
t)
c
∂y(x
,
t)
∂t
+
+
(m
+
+
=
w
(4.7)
∂x
2
∂t
2
∗
Steel railway bridges typically have a very large live load to dead load ratio.