Geology Reference
In-Depth Information
significant loss of information content as long as the fre-
quency of sampling is much higher than the highest
frequency component in the sampled function. Mathe-
matically, it can be proved that, if the waveform is a sine
curve, this can always be reconstructed provided that
there are a minimum of two samples per period of the
sine wave.
Thus, if a waveform is sampled every two milliseconds
(sampling interval), the sampling frequency is 500 sam-
ples per second (or 500 Hz). Sampling at this rate will
preserve all frequencies up to 250 Hz in the sampled
function.This frequency of half the sampling frequency
is known as the
Nyquist frequency
(
f
N
) and the
Nyquist
interval
is the frequency range from zero up to
f
N
(a)
(b)
f
N
=
12
D
t
(
)
(2.2)
where
D
t
= sampling interval.
If frequencies above the Nyquist frequency are pre-
sent in the sampled function, a serious form of distortion
results known as
aliasing
, in which the higher frequency
components are 'folded back' into the Nyquist interval.
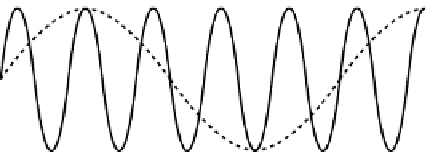
Consider the example illustrated in Fig. 2.3 in which
sine waves at different frequencies are sampled. The
lower frequency wave (Fig. 2.3(a)) is accurately repro-
duced, but the higher frequency wave (Fig. 2.3(b), solid
line) is rendered as a fictitious frequency, shown by the
dashed line, within the Nyquist interval. The relation-
ship between input and output frequencies in the case of
a sampling frequency of 500 Hz is shown in Fig. 2.3(c). It
is apparent that an input frequency of 125 Hz, for exam-
ple, is retained in the output but that an input frequency
of 625 Hz is folded back to be output at 125 Hz also.
To overcome the problem of aliasing, the sampling
frequency must be at least twice as high as the highest fre-
quency component present in the sampled function. If
the function does contain frequencies above the Nyquist
frequency determined by the sampling, it must be passed
through an
antialias filter
prior to digitization. The
antialias filter is a low-pass frequency filter with a sharp
cut-off that removes frequency components above the
Nyquist frequency, or attenuates them to an insignificant
amplitude level.
(c)
f
N
2
f
N
3
f
N
4
f
N
250
125
0
125
250
500
625
750
1000
Input frequency (Hz)
Fig. 2.3
(a) Sine wave frequency less than Nyquist frequency.
(b) Sine wave frequency greater than Nyquist frequency (solid
line) showing the fictitious frequency that is generated by aliasing
(dashed line).
(c) Relationship between input and output frequencies for a
sampling frequency of 500 Hz (Nyquist frequency
f
N
= 250 Hz).
that are non-repetitive. By means of the mathematical
technique of
Fourier analysis
any periodic waveform,
however complex, may be decomposed into a series of
sine (or cosine) waves whose frequencies are integer
multiples of the basic repetition frequency 1/
T
, known
as the
fundamental frequency
.The higher frequency com-
ponents, at frequencies of
n/T
(
n
= 1, 2, 3, . . .), are
known as harmonics. The complex waveform of Fig.
2.5(a) is built up from the addition of the two individual
sine wave components shown.To express any waveform
in terms of its constituent sine wave components, it is
necessary to define not only the frequency of each com-
ponent but also its amplitude and phase. If in the above
example the relative amplitude and phase relations of
the individual sine waves are altered, summation can
2.3 Spectral analysis
An important mathematical distinction exists between
periodic waveforms
(Fig. 2.4(a)), that repeat themselves at a
fixed time period
T
, and
transient waveforms
(Fig. 2.4(b)),