Environmental Engineering Reference
In-Depth Information
between the spring stress and pore-water pressure increment
in the second layer. The rates of strain for the second layer
can be rewritten in terms of the water phase dashpot con-
stant and the spring constants corresponding to the water
phase and the soil structure:
σ
σ
z
(
t
)
1
η
w
η
a
k
w
k
a
c
w
c
a
c
z
(
t
)
2
η
w
η
a
κ
w
z
1
−
z
2
=
κ
w
z
2
−
z
3
+
k
w
k
c
w
+
κ
w
η
w
z
2
˙
(16.100)
c
w
c
w
c
a
z
(
t
)
3
Similar equations can be written for the third and subse-
quent layers. For the
n-
th layer,
κ
w
z
n
−
1
−
z
n
=
c
w
+
κ
w
z (t)
κ
w
z
n
+
η
w
z
n
˙
(16.101)
n
η
w
η
c
w
a
k
w
k
a
c
c
Equations 16.99-16.101 represent a system of linear differ-
ential equations for the linear rheological element associated
with the stress state variable
σ
w
a
(
σ
- u
)
(
σ
- u
)
w
w
u
w
of the unsaturated soil.
The system of linear differential equations for the response
of the linear rheological element associated with the stress
state variable
σ
−
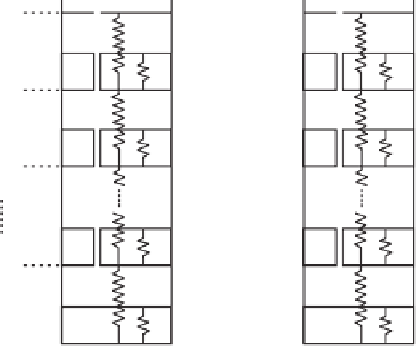
Figure 16.66
Use of linear rheological models to simulate effect
of
σ
−
u
w
and
σ
−
u
a
stress state variables.
−
u
w
can be written in matrix form as
z
0
z
˙
=
Az
+
b
z(
0
)
=
(16.102)
other layers are a slight modification of a linear rheological
element in that the pressure in one piston is fed into the adja-
cent piston in a series manner. The water phase differential
equations can be written as
where
⎡
⎤
−
1100
···
0
˙
z
i
+
1
⎣
⎦
κ
w
c
w
1
−
210
···
0
˙
ε
i
=−
z
i
−˙
i
=
1
,
2
,...,n
−
1
(16.96)
κ
w
c
w
η
w
κ
w
+
···
···
···
···
···
···
A
=
c
w
···
···
···
···
···
···
c
w
˙
0
κ
w
ε
n
=−
˙
z
n
−
(16.97)
0
···
···
1
−
21
0
···
···
01
−
2
⎡
⎤
where:
1
0
·
·
0
⎣
⎦
z
1
(t), z
2
(t),...,z
n
(t)
=
positions of
the
n
pistons,
σc
w
η
w
κ
w
+
respectively, and
b
=
c
w
ε
1
(t), ε
2
(t),...,ε
n
(t)
=
strains of the
n
pistons, respec-
tively.
⎡
⎤
In the first layer of the linear rheological element asso-
ciated with the stress state variable
σ
n
⎣
⎦
u
w
, the total stress
σ
is divided between the pore-water pressure and the stress
acting in the spring representing the soil structure. That is,
−
n
−
1
σ
κ
w
+
·
·
1
z
0
=
c
w
κ
w
z
1
−
z
2
+
η
w
˙
ε
n
σ
=
z
1
−˙
ε
1
−˙
ε
2
−···− ˙
(16.98)
Substituting Eqs. 16.96 and 16.97 into the conservation
equation 16.98 gives
z
0
) is due to the
compressibility of water. If water is assumed to be incom-
pressible, the
c
w
term goes to infinity and
z
0
becomes a
zero vector and the system of linear differential equations
reduces to the equation for the Kelvin model for saturated
soils (Xing et al., 1995).
The system of linear differential equations for the linear
rheological element associated with the stress state vari-
able
σ
The nonzero initial condition (i.e.,
z(
0
)
=
κ
w
z
1
−
z
2
+
c
w
+
κ
w
σ
=
η
w
z
1
˙
(16.99)
c
w
The total stress
σ
also acts on the second piston associated
with the linear rheological element for the stress state vari-
able (
σ
u
w
) of the second layer. However, the Hookean
stress
κ
w
(z
1
−
−
z
2
)
developed in the first layer is the only
stress which causes the piston in the element of the sec-
ond layer to move downward. This stress is again divided
u
a
has the same form as Eq. 16.102 for the stress
state variable
σ
−
−
u
w
with the subscript
w
replaced by the
subscript
a
.

















Search WWH ::

Custom Search