Environmental Engineering Reference
In-Depth Information
c
v
Rearranging the above equation results in a consolida-
tion equation similar in form to Terzaghi's one-dimensional
consolidation equation:
=
coefficient of consolidation with respect to the air
phase, that is,
D
a
(ω
a
/RT
K
)
1
.
u
a
m
1
k
(
1
m
2
/m
1
k
)
¯
−
−
(
1
−
S)n
D
d
ω
a
/RT
K
∂
2
u
a
∂y
2
∂u
a
∂t
1
m
1
k
¯
=
(16.33)
The coefficient of transmission
D
a
is a function of matric
suction and may vary in the
y
-direction. The variation in
transmissivity of the air phase is taken into account in
the last term in Eq. 16.35. There are several relationships
describing the variation of air transmissivity with matric
suction. However, if the variation of air transmissivity with
space is negligible (i.e.,
∂D
a
/∂y
is negligible), Eq. 16.35
can be simplified as follows:
u
a
+
n
The above equation describes the pore-air pressure
changes during one-dimensional consolidation of a dry,
compressible soil. Only air flow occurs during the
consolidation process. The coefficients used in Eq. 16.33
are similar in form to those used in the coefficient of
consolidation
c
v
. In the case where the soil
is dry and
incompressible (i.e.,
m
1
k
=
m
1
k
=
0), Eq. 16.33 reverts to
the equation proposed by Blight (1971):
∂
2
u
a
∂y
2
∂u
a
∂t
∂u
w
∂t
c
v
=−
C
a
+
(16.36)
D
d
/n
ω
a
/RT
K
∂
2
u
a
∂y
2
∂u
a
∂t
=
(16.34)
16.3 SOLUTION OF CONSOLIDATION
EQUATIONS USING FINITE DIFFERENCE
TECHNIQUE
16.2.11 Special Case of Unsaturated Soil
It is possible for air and water to flow simultaneously dur-
ing the consolidation process in an unsaturated soil. The air
phase consolidation equation (i.e., Eq. 16.31) can be written
in a simplified form:
The finite difference technique can be used to solve
unsteady-state (i.e., transient) air flow and water flow
equations associated for one-dimensional consolidation. The
air flow and water flow PDEs can be solved simultaneously
using an explicit forward-marching, finite difference
technique, as illustrated in Fig. 16.3. The finite difference
equations can be written in linear forms for the air and water
phase partial differential flow equations (Dakshanamurthy
and Fredlund, 1981).
Let us consider one-dimensional consolidation where air
flow and water flow occur simultaneously. The spatial vari-
ations of the water coefficient of permeability and the air
∂
2
u
a
∂y
2
c
v
D
a
∂D
a
∂y
∂u
a
∂t
=−
∂u
w
∂t
+
∂u
a
∂y
c
v
C
a
+
(16.35)
where:
C
a
=
interactive constant associated with the air phase
PDE, that is,
(m
2
/m
1
k
)/
[1
m
2
/m
1
k
−
−
(
1
−
S)n
/
u
a
m
1
k
)
], and
(
¯
Time scale (
j
)
z
u
(
i
+ 1,
j
- 1)
w
u
(
i
,
j
- 1)
i z
u
(
i
,
j
)
w
w
u
(
i
- 1,
j
- 1)
H
w
j
t
Water phase
t
Time scale (
j
)
z
u
(
i
+ 1,
j
- 1)
a
u
(
i
,
j
- 1)
i z
a
u
a
(
i
,
j
)
u
(
i
- 1,
j
- 1)
H
a
j t
Air phase
t
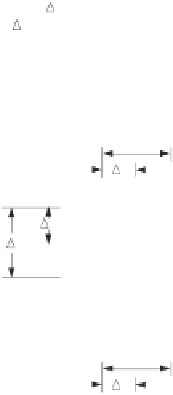
Figure 16.3
Finite difference mesh for solving equations for unsteady-state flow of air and
water.

































Search WWH ::

Custom Search