Mathematisches Rüstzeug - Computergrafik fur Ingenieure - page 338

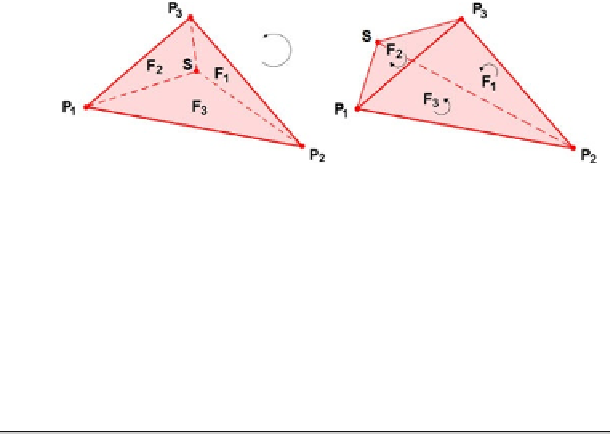
Abb. 11.18 Umfahrungssinn und Schnittpunkt S

dann ergibt sich für die Teilflächen Folgendes:

Fläche S liegt innerhalb außerhalb Dreieck:

F3 1-2-S !g 1-2-S !gpositive

F1 2-3-S !gpositive Teilflächen 2-3-S !gpositive

F2 3-1-S !g 3-1-S !gnegative Teilfläche

Links in Abb. 11.18 ist der Umfahrungssinn bei allen drei Teildreiecken gleich,
und es gilt hier wie zuvor † F k D F mit S im Inneren. Rechts in Abb. 11.18 liegt
S außerhalb und es ändert sich für ein Dreieck der Umfahrungssinn gegenüber
den beiden anderen Dreiecken mit der Folge, dass sich das Vorzeichen von F 2
ändert. Verschiedenes Vorzeichen der Teilflächen ist ein erster Schalter dafür,
dass S außerhalb liegt. Da die Vorzeichen der Teilflächen aber nicht weiter von
Belang sind, bildet man die natürlichen Koordinaten wie angegeben zu • k D
F k = F. Bei †• k >1 liegt der Punkt S außerhalb, bei †• k D 1 innerhalb des
Dreiecks. Ist ein • k D 0 , liegt S auf einer Kante und die Teilung entspricht
einer linearen Interpolation entlang der Kante. Bei zwei • k D 0 liegt S in einem

Knoten, trotzdem ist in beiden Fällen †• k D 1 .

11.3.11 Transformation von Normalenvektoren {n}

Die Szenerie wird normalerweise in einer Reihe von unterschiedlichen Viewpositio-
nen betrachtet. Die zugehörigen Transformationen bearbeiten dabei nur die Knoten.
Die Facetten bleiben unverändert und werden sozusagen in die neuen Positionen der
Knoten eingehängt. Die schon berechneten Normalenvektoren sind danach nicht
mehr gültig und müssen neu berechnet werden.
Die aufwendige Variante berechnet die Normalenvektoren völlig neu aus den
neuen Knotenkoordinaten der Facetten. Es lässt sich aber auch eine Transformati-
onsmatrix [M] finden, mit der die Normalenvektoren in die neue Projektion umge-
rechnet werden und dann wieder zu den Facetten „passen“.
Ausgangspunkt ist hier das Skalarprodukt eines beliebigen Vektors f v g in der
Ebene und des Normalenvektors f n g . Das Skalarprodukt ist dann für die Ausgangs-