Graphics Reference
In-Depth Information
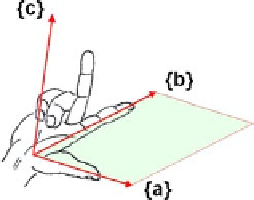
Abb. 11.4
„Rechts“system der rechten Hand
11.1.6 Vektorprodukt
Das vektorielle Produkt
f
a
gf
b
g
zweier Vektoren
f
a
gD.
a
x
,a
y
,a
z
/
und
f
b
gD
.
b
x
,b
y
,b
z
/
ist definiert als ein Vektor
f
c
g
mit folgenden Komponenten:
c
x
D
a
y
b
z
a
z
b
y
c
y
D
a
z
b
x
a
x
b
z
c
z
D
a
x
b
y
a
y
b
x
f
a
gf
b
gDf
c
g!
Die Länge
j
c
j
des Ergebnisvektors
f
c
g
entspricht dem Flächeninhalt des von
f
a
g
und
f
b
g
gebildeten Parallelogramms. Des Weiteren ist
f
c
g
ein
Normalen
vektor, der auf
der von
f
a
g
und
f
b
g
aufgespannten Ebene senkrecht steht. Seine Orientierung ist
dadurch festgelegt, dass die drei Vektoren ein „Rechts“system wie die drei Finger
der rechten Hand bilden (Abb.
11.4
).
Normiert man die Komponenten c
k
mit der Länge |c|, dann erhält man einen auf
der Ebene senkrecht stehenden Einheitsvektor. Hiervon wird in der Grafikprogram-
mierung häufig Gebrauch gemacht.
Es gelten folgende Rechengesetze:
f
a
gf
b
gDf
b
gf
a
g
.
u
f
a
g/f
b
gD
u
.f
a
gf
b
g/
f
c
g.f
a
gCf
b
g/ Df
c
gf
a
gCf
c
gf
b
g
f
a
gf
a
gDf
0
g
f
a
gf
b
gDf
0
g
falls
f
b
g
zu
f
a
g
parallel/antiparallel
:
Das
{0}
-Ergebnis ist ebenfalls in der Grafikprogrammierung interessant, um par-
allele Vektoren zu finden. Das Vektorprodukt gilt nur im 3-dimensionalen, das
Skalarprodukt jedoch im n-dimensionalen Raum.
Im Vorgriff auf die Arbeit mit Matrizen wird das Vektorprodukt alterna-
tiv als Matrixmultiplikation dargestellt. Hierzu wird mit dem Vektor
{a}
eine
schief-symmetrische Matrix wie folgt aufgebaut und diese mit dem Vektor
{b}
multipliziert. Der Ergebnisvektor ist das Vektorprodukt: