Graphics Programs Reference
In-Depth Information
Tangent line
f
(
x
)
Figure 4.4.
Graphical interpretation of the Newton-Raphson
formula.
f
(
x
i
)
x
x
x
+1
i
i
Agraphical depiction of the Newton-Raphson formulais shown in Fig. 4.4. The for-
mula approximates
f
(
x
) by the straight linethat istangent to the curve at
x
i
. Thus
x
i
+
1
is at the intersection of the
x
-axis and the tangentline.
The algorithm for the Newton-Raphsonmethodissimple:it repeatedly applies
Eq. (4.3), starting with an initial value
x
0
, until the convergence criterion
|
x
i
+
1
−
x
1
|
<ε
is reached,
being the error tolerance. Only the latest valueof
x
hastobe stored. Here
is the algorithm:
ε
1.
Let
x
be aguess for the root of
f
(
x
)
=
0.
f
(
x
).
2. Compute
x
=−
f
(
x
)
/
|
|
<ε
3.
Let
x
←
x
+
x
and repeat steps 2-3until
x
.
f
(
x
)
f
(
x
)
x
x
x
x
1
0
2
x
x
0
(a)
(b)
Figure
4.5.
Examples where
the
Newton-Raphsonmethod
diverges.
Although the Newton-Raphsonmethod converges fast near the root, its global
convergence characteristics are poor. The reasonisthat the tangentline is not al-
ways an acceptable approximation of the function, as illustratedinthe twoexamples
inFig. 4.5. But themethod canbemade nearly fail-safe by combining it with bisection,
as in Brent's method.
newtonRaphson
The following
safe version
of the Newton-Raphsonmethodassumes that the root
to becomputedis initiallybracketedin
(a,b)
. The midpointofthebracket is used
as the initial guess of the root. The brackets are updatedafter each iteration. If a


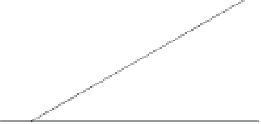









Search WWH ::

Custom Search