Graphics Programs Reference
In-Depth Information
4.4
Brent's Method
Brent's method
7
combines bisection and quadratic interpolationinto an efficient
root-finding algorithm. Inmost problems the methodis much faster than bisection
alone, but itcan becomesluggish if the functionis not smooth. It is the recommended
method of root finding if the derivative of the functionis difficult or impossible to
compute.
f
(
x
)
f
(
x
)
Old interval
New
interval
Old interval
New
interval
x
x
x
1
x
3
x
1
x
x
x
x
x
2
3
2
(a) Case of
x < x
Figure 4.2.
Inverse quadratic iteration.
(b) Case of
x > x
3
3
Brent's methodassumes that aroot of
f
(
x
)
=
0has been initiallybracketedin
the interval(
x
1
,
x
2
). The root-finding process starts with abisection step thathalves
the intervaltoeither (
x
1
,
2, as shown in Figs. 4.2(a)
and (b). In the course of bisectionwehad to compute
f
1
=
x
3
)or (
x
3
,
x
2
), where
x
3
=
(
x
1
+
x
2
)
/
f
(
x
1
),
f
2
=
f
(
x
2
) and
f
(
x
3
), so that we now know three points on the
f
(
x
)curve (the open circles in
the figure). These points allowustocarry out the next iteration of the root by
inverse
quadratic interpolation
(viewing
x
as a quadraticfunction of
f
). If the result
x
of the
interpolation falls inside the latest bracket (as is the case in Figs. 4.2), we accept the
result. Otherwise, anotherround of bisectionis applied.
f
3
=
f
(
x
)
f
(
x
)
x
x
3
x
x
1
1
3
x
x
x
x
2
2
(a)
(b)
Figure 4.3.
Relabeling points afteraniteration.
The next stepistorelabel
x
as
x
3
and rename the limits of the newinterval
x
1
and
x
2
(
x
1
<
x
2
), as indicatedinFigs. 4.3. Wehave nowrecovered the orig-
inal sequencing of points in Figs. 4.2, but the interval(
x
1
,
x
3
<
x
2
)containing the root
7
Brent, R. P.,
Algorithms for Minimization without Derivatives
,Prentice-Hall, 1973.











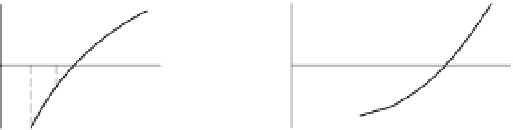












Search WWH ::

Custom Search