Graphics Programs Reference
In-Depth Information
1.00
l
2
0.50
l
1
0.00
l
3
-0.50
0.00
0.50
1.00
1.50
2.00
2.50
3.00
x
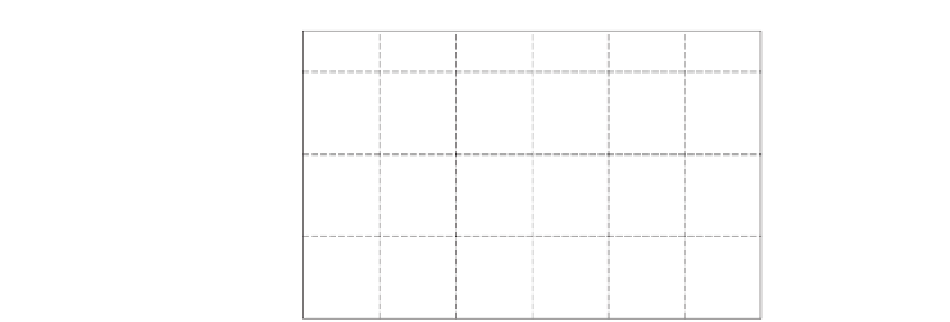
Figure 3.2.
Example of quadraticcardinalfunctions.
To provethat the interpolating polynomial passes through the datapoints, we
substitute
x
=
x
j
into Eq. (3.1a) and thenutilize Eq. (3.2). The result is
n
n
P
n
−
1
(
x
j
)
=
y
i
i
(
x
j
)
=
y
i
δ
i j
=
y
j
i
=
1
i
=
1
It can be shown that the errorinpolynomial interpolationis
(
x
−
x
1
)(
x
−
x
2
)
...
(
x
−
x
n
)
f
(
n
)
(
f
(
x
)
−
P
n
−
1
(
x
)
=
ξ
)
(3.3)
n
!
where
x
n
);its value is otherwise unknown. It is
instructivetonote that the fartheradatapoint isfrom
x
, the more itcontributes to
the errorat
x
.
ξ
lies somewhere in the interval(
x
1
,
Newton's Method
Evaluation of polynomial
Although Lagrange's methodisconceptually simple, it does not lend itself to an effi-
cient algorithm. Abetter computational procedure isobtainedwith Newton'smethod,
where the interpolating polynomial is writteninthe form
P
n
−
1
(
x
)
=
a
1
+
(
x
−
x
1
)
a
2
+
(
x
−
x
1
)(
x
−
x
2
)
a
3
+···+
(
x
−
x
1
)(
x
−
x
2
)
···
(
x
−
x
n
−
1
)
a
n
This polynomiallends itself to an efficientevaluationprocedure.Consider,for
example, four datapoints (
n
=
4). Here the interpolating polynomial is
=
a
1
+
−
x
1
)
a
2
+
−
−
x
2
)
a
3
+
−
−
−
P
3
(
x
)
(
x
(
x
x
1
)(
x
(
x
x
1
)(
x
x
2
)(
x
x
3
)
a
4
=
a
1
+
(
x
−
x
1
)
{
a
2
+
(
x
−
x
2
) [
a
3
+
(
x
−
x
3
)
a
4
]
}









Search WWH ::

Custom Search