Cryptography Reference
In-Depth Information
We next observe that |{i : k
i
= x}|≤
x
, for x ∈{1,...,r}. This observa-
tion enables the following upper bound:
r
X
X
x
·
1
r
k
·
1
1
2
x−1
≤ 2r
2
k
≤ 2r ln 2 ≈ 1.38·r
x=1
x=1
This completes the proof.
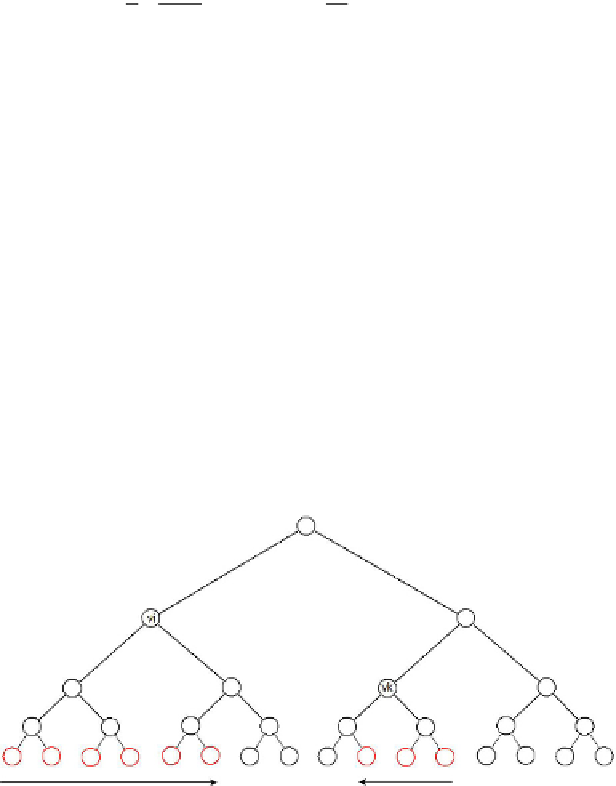
2.5.3 Key Chain Tree
In this section we will describe the key-chain tree set system Φ
KCT
. Con-
sider again a binary tree whose leaves correspond to the receivers in the user
population [n] = {1,...,n} where n is considered a power of 2. For each inter-
nal node v
i
of the binary tree, consider the sequence of consecutive leaves of
the tree rooted at v
i
. Any consecutive sequence starting from the leftmost or
rightmost leaf of the tree rooted at v
i
amounts to a subset in the set system.
See the figure
2.15
for two examples of subsets in the set system. With this
description, it is not hard to observe that there are lists of leaves in the binary
tree starting from the leftmost (resp. rightmost) leaf of an intermediate node
v
i
that will also yield a subset due to the node v
j
if v
j
is a left (resp. right)
child of v
i
. Hence, each subset is being considered more than once depend-
ing on the geometry of its leaves, which results an unnecessary increase in
key-storage unless some special care is taken.
Fig. 2.15. An example of a subset in the Key Chain Tree method.
For the sake of avoiding the extra counting we define the following notion:
we say a a pair of nodes (u
1
,u
2
) is related to an intermediate node v if the
following hold: (i) v is the least-common ancestor of u
1
and u
2
and (ii) it holds
that either u
1
is the leftmost leaf or u
2
is the rightmost leaf of the tree rooted
at node v. We consider the pairs that can be related to an intermediate node
as the subsets of the Key Chain Tree. This will be su
ce to count each subset
once.