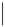Cryptography Reference
In-Depth Information
PatternCover
(Subset Collection Φ)
1. P = ∅
2. Repeat the following steps until break.
3. u = Φ.slo(P), let s = {u}
4. if u =⊥ then output P and break.
5. Repeat the following steps until s does not change.
6. Find y = Φ.cvr(s,i) for minimal i ≤ Φ.cvm such that y 6= ⊥
7. if it exists.
8. if y 6= ⊥ then s = y
9. P = P∪s
Fig. 2.8. A
PatternCover
algorithm that works optimally for separable set systems.
Proof. Theorem
2.29
Note that the algorithm in Figure
2.8
, starts from an
atom in the poset of subset collection Φ and “grows” the current element until
it hits the top of the ideal the selected atom was in. In the next iteration,
another atom is selected outside the ideals so far included in the broadcast
pattern. These ideals are actually the ones that make up the lower-maximal
partition of the set system Φ. Overall, the algorithm will return the set of
upper bounds from each ideal, i.e., their principal elements, which result in,
of course, the optimal solution with size ord(Φ). This is because, the optimal
solution requires at least one element from each ideal necessarily.
The running time of the algorithm in Figure
2.8
is bounded by the sum of
the chains followed by Φ.cvr() in each of the ideals that comprise the lower
maximal partition of Φ. Typical collections (see next section) have chains of
polylogarithmic length in the number of users and thus the running time of the
algorithm is quite e
cient. The parent finding procedure cvr(·,·) of the set
system plays an important role in this algorithm. Note that the
PatternCover
algorithm looks for a parent with a maximal size out of at most Φ.cvm possible
choices.
Factorizable Families.
We next introduce a basic property regarding the ideals of a family Φ that will
play an important role in solving optimally the revocation problem. Intuitively
the factorizable property mandates that the complements of the atomic filters
in (Φ,⊆) share some similar properties to prime ideals over rings. We use the
notation (S) to denote the principal ideal of S ∈ Φ.
Definition 2.30. A fully-exclusive set system Φ is called factorizable if the
poset, itself, is separable and for any subset S ⊆ Φ and any atom u, it holds
that (S) ∩P
u
is a separable set.
In the following lemma we present some useful facts about the P
u
sets and
the factorizable property.