Efficient Pairing Computation on Elliptic Curves in Hessian Form - Information Security and Cryptology-ICISC 2010 - page 173

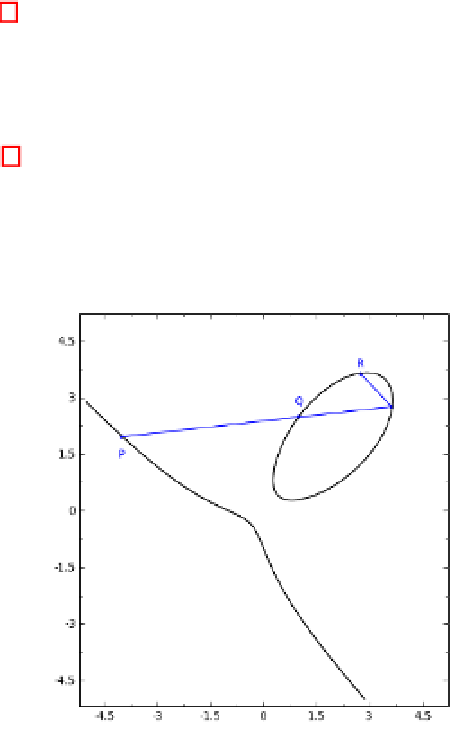
By Theorem 1, we can know the geometric interpretation of the group law on
Hessian curves.
Suppose P, Q are two points on a Hessian curve. The sum R ,of P and Q ,
is defined as follows. First draw a line through P and Q which intersects the
Hessian curve at a third point. Then R is the reflection of this point about the
line y = x . Fig. 1 depicts the addition on x 3 + y 3 +1=7 xy over real field.
The double R , of P, is defined as follows. First draw the tangent line to the
curve at P . The line intersects the curve at a second point. Then R is the
reflection of this point about the line y = x .

Fig. 1. Point addition on x 3 + y 3 +1=7 xy over R

4 Formulas for Pairings on Hessian Curves

Similarly to Eq. (1), using Theorem 1, we can prove the relation

f i + j,P = f i,P · f j,P · g iP,jP

on Hessian curves. This means pairings on Hessian curves can be computed by
Miller's algorithm [17].
In most cryptographic protocols, P canbechosensuchthat <P > is the
unique subgroup of order r in

H ( F p ). Suppose the embedding degree k is even,

then the field extension F p k is usually constructed via a quadratic subfield as

F p k/ 2 ( α ), with α 2 F p k = = δ ∈ F p k/ 2 .Since k is the smallest positive integer

( p k 1), it follows that ( p k 1) /r is a multiple of p u such that r | − − − 1forsome

F p u proper divisor u of k . So all elements of map to 1 when raised to the power

( p k 1) /r .

Without loss of generality, we suppose d

−

∈ F p k/ 2 , and select a ∈ F p k/ 2 ran-

such that ( a + bα ) 3 +( a bα ) 3 +1= domly. Repeat a = a +1until ∃ b ∈ F p k/ 2 −