Cryptography Reference
In-Depth Information
and SK-ID-KEM [12] to fit the twin BDHI problem, yielding twin SK-IBE
and twin SK-ID-KEM, which outperform the original schemes in terms of
eciency especially for security analysis. A comparison to prior schemes is
shown in Table 1.
Table 1.
Comparison to prior schemes
Scheme
Type
Ciphertext size Key size Enc
Dec
Reduction factor
Chen et al.[11]
IBE
|
G
|
+2
|
G
|
2E 1E+1P 1
/Q
h
1
Q
h
2
(
Q
h
3
+
Q
h
4
)
Ours
IBE
2
|
G
|
+2
2
|
G
|
4E 2E+2P
1
/Q
h
1
Chen et al.[12] ID-KEM
|
G
|
+
|
G
|
2E 1E+1P 1
/Q
h
1
Q
h
2
(
Q
h
3
+
Q
h
4
)
Ours
ID-KEM
2
|
G
|
+
2
|
G
|
4E 2E+2P
1
/Q
h
1
P denotes a pairing operation, and E a group exponentiation in
G
or
G
T
.Acom-
=2
60
for 1
mon estimate used here are
Q
h
i
≤ i ≤
4 (suggested by Bellare and
Rogaway [4]).
Judging from appearances our schemes seem to be less ecient because our
schemes double the number of group exponentiations and pairing operations in
computation overheads and increase one group element in the ciphertext, one
group element in the private key. Before illustrating why our twin schemes are
more ecient than prior schemes at the same security level, we first review
the concept of the tightness of security reduction [3, 19]. Consider a scheme
with a security reduction showing that an adversary attacking the scheme in
time
t
with advantage
implies another adversary breaking some intractable
problem in time
t
+
ω
1
with advantage
≥
/ω
2
. The tightness of security
reduction refers to the values of
ω
1
and
ω
2
. If the underlying assumptions are
the same, the scheme with a looser security reduction needs to increase the
size of the groups to obtain the same security level of the one with a tighter
security reduction. Using the general method, exponentiations and pairings in a
group whose elements can be represented in
r
bits takes roughly
(
r
3
)time.Asa
concrete example, performing two 128-bit group exponentiations/pairings can be
significantly faster than a single 256-bit group exponentiation/pairing. From the
comparison in Table 1, we learn that to obtain the same security guarantee, the
group size of [11] and [12] is roughly 120 bits larger than the size of our schemes.
Therefore at the same security level, our twin schemes are more ecient than
prior schemes while the ciphertext size and the key size are roughly the same.
O
2
The Twin Bilinear Die-Hellman Inversion
Assumption
In this section, we introduce the twin bilinear Die-Hellman inversion problem.
Let us first review some necessary facts about bilinear maps. Suppose
G
and
G
T
are two multiplicative groups of prime order
p
,and
g
is the generator of
G
.The
groups are equipped with a map
e
:
G
×
G
→
G
T
which satisfies the following
properties:

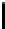





























Search WWH ::

Custom Search