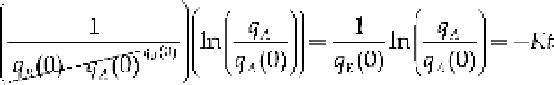Biochemical Reactions and Enzyme Kinetics - Introduction to Biomedical Engineering - page 452

q A ¼0 ¼ q A ¼0 ¼

1
q A q A q A ð

1 1

B 2 ¼ q A

ð 0 Þþ q B ð 0 Þ Þ ð q A q A ð 0 Þþ q B ð 0 Þ Þ q A ð 0 Þ q B ð 0 Þ

Integrating both sides of Eq. (8.5) gives

ln

1 q A q A ð 0 Þþ q B ð 0 Þ q A

q A ð

ln ¼ Kt ð 8 : 6 Þ

q A ð 0 Þ q B ð 0 Þ q B ð 0 Þ 0 Þ

and after algebraically manipulating, we have

ð q A ð 0 Þ q B ð 0 Þ Þ

q A ¼ ð 8 : 7 Þ

Þ e Kq A ð0Þ q B ð0Þ

ð Þ t

q B ð 0

1

q A ð

0 Þ

One final note regarding the solution of Eq. (8.2) is to consider the case in which
q B ð

0 Þ q A ð 0 Þ . Here, the change in q B is small compared to q B ð 0 Þ , and q B can be treated

essentially as a constant—that is, q B ¼ q B ð 0 Þ . Thus, an approximation to Eq. (8.2) is

q A ¼ Kq B q A ¼ Kq B ð

0 Þ q A ð 8 : 8 Þ

which can be straightforwardly solved as

Þ e Kq B ð0Þ t u ð t Þ q A ¼ q A ð 0 ð 8 : 9 Þ

Þ e Kq B ð0Þ t Substituting Eq. (8.9) into

q P ¼ Kq B q A ¼ Kq B ð

0 Þ q A ¼ Kq B ð 0 Þ q A ð 0 and integrating

gives

e Kq B ð0Þ t

q P ¼ q A ð 0 Þ 1 u ð t Þ ð 8 : 10 Þ

It should be clear that the steady-state value of q P equals q A ð 0 Þ:

Let us take another look at the solution in Eq. (8.7) for q A , and compare it to that of Eq. (8.9)

by assuming that q B ð 0 Þ q A ð 0 Þ , which gives the approximation q B ¼ q B ð 0 Þ , and thus

¼

q A q A ð 0 Þþ q B ð 0 Þ q B ð 0 Þ

q A q A ð 0 Þ¼ q B q B ð 0 Þ¼ 0. Hence, we have ln ¼ ln 0, and

q B ð 0 Þ q B ð 0 Þ

therefore Eq. (8.7) becomes

ð 8 : 11 Þ

Rearranging and taking the exponential of both sides gives

Þ e Kq B ð0Þ t u ð t Þ q A ¼ q A ð 0 ð 8 : 12 Þ

which is the result we found in Eq. (8.9). In terms of the body, many small molecules like
glucose and other nutrients are available in large quantities as compared with other reac-
tants. Thus, this simplification is often quite appropriate.