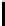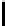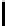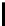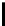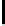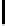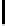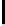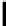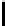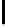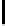Cryptography Reference
In-Depth Information
y
0
1
2
3
4
5
6
7
f
y
106
166
132
200
238
93
158
129
S
256
[y]
230
166
87
48
238
93
68
239
y
8
9
10
11
12
13
14
15
f
y
202
245
105
175
151
229
21
142
S
256
[y]
202
83
105
147
151
229
35
142
The key recovery strategy is as follows. Consider all possible systems of 5
equations chosen from the 16 equations of the form S
N
[y] = f
y
, 0 ≤ y ≤ 15.
A solution to such a system would give one candidate key. The correctness of a
candidate key can be verified by running the KSA with this key and comparing
the permutation thus obtained with the permutation in hand. Of course, some
of the systems may not be solvable at all.
The correct solution for this example correspond to the choices y = 1,4,5,8
and 12, and the corresponding equations are:
K[0] + K[1] + (12)/2
=
166
K[0] + K[1] + K[2] + K[3] + K[4] + (45)/2
=
238
K[0] + ... + K[5] + (56)/2
=
93
K[0] + ... + K[8] + (89)/2
=
202
K[0] + ... + K[12] + (1213)/2
=
151
The correctness of a solution depends on the correctness of the selected
equations. The probability that we would indeed get a correct solution from
a system is equal to the joint probability of S
r
[y] = f
y
for the set of chosen
y-values. However, we do not need the assumption that the majority of the
equations are correct. Whether a system of equations is correct or not can be
cross-checked by running the KSA again. Moreover, empirical results show
that in a significant proportion of the cases one might obtain enough correct
equations to have the correct key as one of the solutions.
The exhaustive search for a 5-byte key requires a complexity of 2
40
.
Whereas in the above approach, one needs to consider at the most
16
5
=
4368 < 2
13
sets of 5 equations. Since the equations are triangular in form,
solving each system of 5 equations would take approximately 5
2
= 25 (times
a small constant) < 2
5
many additions/subtractions. Thus the improvement
over exhaustive search is almost by a factor of
2
40
2
13
2
5
= 2
22
.
Let us now describe the approach in general. Theorem 3.1.5 gives us how
S
r
[y] is biased to different combinations of the keys, namely, with
y
f
y
=
y(y + 1)
2
+
K[x].
x=0
Let us denote
P(S
r
[y] = f
y
) = p
r,y
,
for 0 ≤ y ≤ r−1, 1 ≤r ≤ N.