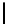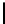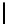Fault Attacks - RC4: Stream Cipher and Its Variants - page 207

average case time complexity of the InvertStuckPRGA algorithm would be re-
duced to O . However, i G must be known to have this advantage.

Since in general i G would not be known to the attacker (see Section 8.4.3 for
details), item 1 of Theorem 8.4.12 is not used in the state recovery strategy.

R 2 N +⌈A⌉!

The quantity log 2 (⌈A⌉!) may be interpreted as a measure of uncertainty
in resolving the permutation. For N = 256, Table 8.2 lists the values of A
and log 2 (⌈A⌉!) for some values of R. Observe that if all the successors are
unresolved (e.g. the case R = 1), the uncertainty is log 2 (256!) ≈ 1683.9961.

Runs Avg. No. of Elements with Uncertainty in Permutation

R Unassigned Successors A log 2 ( ⌈A⌉ !)

1 256 1684

2 94.73 491.69

3 35.05 138.09

4 12.97 32.54

5 4.80 6.91

6 1.78 1.00

7 0.66 0.00

8 0.24 0.00

TABLE 8.2: Decrease in uncertainty of resolving the permutation with in-
creasing runs

The data indicates that as one considers more number of runs, the uncer-
tainty in resolving the permutation is reduced. In fact, the uncertainty starts
decreasing when only the first 258 keystream output bytes are available, as
z 1 and z 258 come from the same index a 0 + a 1 (see Table 8.1) and form a
candidate pair. Table 8.2 also shows that theoretically 7 runs are enough to
shrink the uncertainty in resolving the permutation to zero and recover the
permutation in O(R 2 N) time. However, empirical results confirm that 8 runs
provide a conservative estimate, after which there is no uncertainty in resolv-
ing the permutation. Zero uncertainty implies that the permutation obtained
after ResolveConflicts in Step 2 of InvertStuckPRGA algorithm is a resolved
permutation. In this case, the time complexity of InvertStuckPRGA reduces
to 8 2 256 = 2 14 .
The permutation can still be completely recovered, even if fewer numbers
of keystream bytes are available. The price to be paid is an increase in time
complexity due to exhaustive assignment of successor elements. For example,
when R = 4, i.e., when we start with the first 1024 keystream output bytes,
the average number of permutation elements whose next entries are not deter-
mined is 256( 255

256 ) 3∗254 = 12.97. If we exhaustively fill in these ⌈12.97⌉ = 13
successor values, we would generate 13! ≈ 2 32 possible resolved permutations.
The time complexity of complete permutation recovery with 1024 keystream
bytes would be around (4 2 + 2 32 )256 ≈ 2 48 .