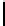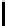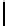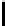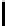Cryptography Reference
In-Depth Information
Corollary 4.7.12. If l ≤ 16 (i.e., the key length is small), then we have
c(δ,t)p
t
q
2
−t
c(δ
′
,t
′
)p
′t
′
q
′
l
2
−t
′
(1−q
d−δ
q
′d−δ
′
),
π
d
≈
δ≤d,δ
′
≤d
t≤
2
−δ,t
′
≤
2
−δ
′
N−2
l
2
−1
where p =
l
y=N−1−
2
p
′
y
, q = 1−p, q
′
= 1−p
′
.
Proof: Approximating each p
y
in the left half by the average p of the
first
y=0
p
y
, p
′
=
l
2
many p
y
's and each p
′
y
in the right half by the average p
′
of the last
2
many p
′
y
's, we get the result. The ranges of the variables in the summation
account for conditions 3 and 6 of Definition 4.7.9. The term c(δ,t)p
t
q
2
−t
accounts for the conditions 1 and 2, the term c(δ
′
,t
′
)p
′t
q
′
l
2
−t
′
accounts for the
conditions 4 and 5, and the term (1 −q
d−δ
q
′d−δ
′
) accounts for the condition
7 of Definition 4.7.9.
A comparison of the theoretical estimates of π
d
from Corollary 4.7.12 with
the experimental values obtained by running the RC4 KSA with 10 million
randomly generated secret keys of length 16 bytes is presented in Table 4.9.
l
d
2
3
4
5
6
Theoretical
0.0055
0.1120
0.3674
0.6194
0.7939
Experimental
0.0052
0.1090
0.3626
0.6152
0.7909
TABLE 4.9: Theoretical and experimental values of π
d
vs. d with l = 16.
The results indicate that the theoretical values match closely with the
experimental values.
Theorem 4.7.13. The number of distinct d-favorable (t,t
′
)-bisequences con-
taining exactly f ≤ 2l filters is
2d−δ−δ
′
2d−δ−δ
′
s
l−2d + δ + δ
′
f −t−t
′
−s
c(δ,t)c(δ
′
,t
′
)
.
δ≤d,δ
′
≤d
s=1
t≤
2
−δ,t
′
≤
2
−δ
′
Proof: By Lemma 4.7.10, the number of distinct sequences of indices in
0,
l
2
N −1−
l
−1
∪
2
,N −2
satisfying the conditions 1 through 6 of Definition 4.7.9 is
c(δ,t)c(δ
′
,t
′
).
δ≤d,δ
′
≤d
t≤
2
−δ,t
′
≤
2
−δ
′
The justification for the two binomial coe
cients with a sum over s is as