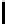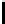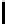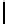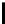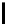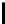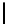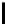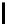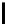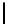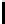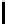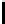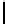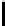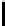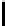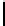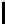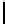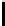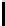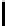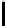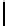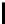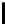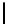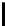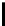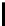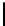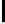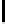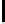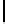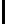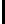Cryptography Reference
In-Depth Information
l
8
10
12
16
Probability
0.4058 0.1290 0.0212 0.0005
Data from [15]
Time in Seconds
0.60
3.93
7.43
278
Probability
0.414
0.162
0.026
0.0006
Results from Table 4.1
2
31.9
2
34.0
2
31.6
2
32.2
Complexity
Probability
0.4362 0.1421 0.0275 0.0007
Exp. I
2
26.8
2
29.9
2
32.0
2
40.0
Complexity
Probability
0.7250 0.2921 0.0659 0.0007
Exp. II
2
40.6
2
40.1
2
40.1
2
40.0
Complexity
Probability
0.931
-
0.506
0.0745
Data from [5]
Time in Seconds
8.602
-
54.390
1572
TABLE 4.8: Experimental results for l = 8,10,12,16.
4.6 Bit by Bit Recovery
The work of Khazaei and Meier [83] starts with the equations
K[y
1
+ 1...y
2
] = C
y
2
−C
y
1
of [15] and considers a bit-by-bit approach to key recovery. We briefly describe
their work below.
The event
−C
y
1
holds with certain probability, say p
y
1
,y
2
. In practice, one can model the above
equation as
K[y
1
+ 1...y
2
] = C
y
2
−C
y
1
+ e
y
1
,y
2
,
where e
y
1
,y
2
is the noise component noise whose distribution depends on p
y
1
,y
2
.
The range of y
1
,y
2
can be written as −1 ≤ y
1
< y
2
K[y
1
+ 1...y
2
] = C
y
2
≤ N − 1, with the
choice C
−1
= 0. Let E
y
1
,y
2
denote the random variables corresponding to the
noises e
y
1
,y
2
. In this setup, the key can be recovered in a correlation-based
attack by using a hypothesis-testing approach. Similar to [168], the authors
of [83] assume that for wrong guess K of the key K, the values C
y
2
−C
y
1
and
K[y
1
+ 1...y
2
] are uncorrelated. Given
N(N+1)
2
samples of
e
y
1
,y
2
= K[y
1
+ 1...y
2
]−(C
y
2
−C
y
1
)
as a realization of the random variables E
y
1
,y
2
, the problem is to decide
whether the guess
K is correct or not. Thus, one needs to test the null
hypothesis
p
y
1
,y
2
for e = 0;
H
0
: K = K,P(E
y
1
,y
2
= e | H
0
) =
1−p
y
1
,y
2
N−1
for 1 ≤ e ≤N −1.