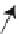Biomedical Engineering Reference
In-Depth Information
alimentary canal. During the heart systole with increased
blood flow, the volume, for example, of a limb increases
due to the inflow of blood (
swelling
). Impedance may in
many cases be regarded as measuring both volume and
flow, a volume change must be due to a flow. Measure-
ments may be based on, for example, mechanical di-
mensional change (strain-gauge plethysmography, light
absorption (photo-plethysmography), X-ray absorption or
immittance change. Application areas are rather diver-
sified, for example, heart stroke volume (SV), cardiac
output (CO), respiration volume, fluid volume in pleural
cavities, edema, urine bladder volume, uterine contrac-
tions, detection of vein thrombosis.
L
Δ
v
L
Figure 4.1-8 Cylinder models of length L and a small parallel
volume increment Dv. Upper: one-compartment, lower:
two-compartment model.
4.1.2.1 Ideal cylinder models
By ideal we mean that the biomaterial is considered in-
compressible and homogeneous. The cross sectional area
of the cylinder may be circular, elliptic or have any plane
form. Estimation of volume from immittance measure-
ment is based on two effects:
1.
A geometry-dependent effect illustrated by the
cylinder model and the ratio
A/L
in the equation
G ¼
s
A/L
. The resulting effect will be dependent on
the constraints on the measured tissue volume: if the
volume increase results in a swelling of length
L
,
conductance will fall. If the volume increase results
in a swelling of cross sectional area
A
, the conductance
will increase. If the volume increase occurs outside
the measured tissue volume, the measured
conductance will not change with the geometrical
volume increase.
2.
A conductivity-dependent component. Of special
interest is the flow dependence of the conductivity of
blood.
versions may be preferred because they lead to simpler
and more exact expressions.
One-compartment model. Cylinder surrounded
by air (cf.
Fig. 4.1-8
top)
In many applications the absolute volume may remain
unknown; the emphasis is instead on the
relative
volume
change
D
y/y. Also the relative conductance change
AG/G
is of special interest, because the ratio is related to the
signal-to-noise ratio which should be as high as possible.
From eq. (
4.1.1
):
DG
G
¼
D
y
DG
D
y
¼
s
or
or
y
L
2
D
y
¼ DG
r
L
2
ð
exact
Þ
(4.1.2)
Thus it is clear that relative volume changes can be
found without knowing the dimensions of the cylinder.
In order to have a high sensitivity (large
DG
) for a given
volume change
D
y, the length
L
should be as short as
possible.
Under the presumption that
L ¼
const. the conduc-
tance model is preferred. If we still use a resistance
model we have from eq.
(4.1.1)
:
D
y
¼
1
For the further analysis of these effects it is useful to
set up some simple cylinder models.
The geometry is shown in
Fig. 4.1-8
. For the single
cylinder shown at the top of
Fig. 4.1-8
the volume
v
is
easily found from
G ¼
s
A/L
or
R ¼
r
L
/
A
:
r
L
2
L
2
s
R þ
D
R
1
y
¼ G
r
L
2
¼ R
s
A
2
¼
1
R
ð
exact
Þ
(4.1.1)
R
¼
DR
R
1
R þ DR
r
L
2
ð
exact
Þ
(4.1.3)
Notice that with the presumption
L ¼
const, the
volume y is proportional to
G
. If the presumption is that
A ¼
const, the volume y is proportional to
R. If swelling is
longitudinal
the volume increase
D
y is best modeled as
a resistance increase in a series model.
If swelling
is transverse
(
as supposed in many cases
), the volume in-
crease
D
y is best modeled as a conductance increase in a
parallel model. If it is not known whether the tissue swells
in longitudinal or transverse direction, the conductance
Equation (
4.1.3
) becomes linear only if
DR R
:
D
yy
DR
r
L
R
2
ðDR RÞ
(4.1.4)
The minus signs in eqs.
(4.1.3) and (4.1.4)
are because
a resistance
increase
corresponds to a volume
decrease
.