Cryptography Reference
In-Depth Information
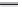
of integer pairs satisfying
m
b
)
has the following properties, which result
immediately from division with remainder:
|
(
a
−
(i)
R
is
reflexive:
For all integers
a
it holds that
(
a, a
)
is an element of
R
,thatis,
we have
a
≡
a
mod
m
.
(ii)
R
is
symmetric:
If
(
a, b
)
is in
R
,thensois
(
b, a
)
; that is,
a
≡
b
mod
m
implies
b ≡ a
mod
m
.
(iii)
R
is
transitive:
If
(
a, b
)
and
(
b, c
)
are in
R
, then so is
(
a, c
)
;thatis,
a ≡ b
mod
m
and
b ≡ c
mod
m
implies
a ≡ c
mod
m
.
The equivalence relation
R
partitions the set of integers into disjoint sets, called
equivalence classes:
Given a remainder
r
and a natural number
m>
0
the set
r
:=
{
a
|
a
≡
r
mod
m
}
,
or, in other notation,
r
+
m
, is called the
residue class
of
r
modulo
m
.Thisclass
contains all integers that upon division by
m
yield the remainder
r
.
Here is an example: Let
m
=7
,
r
=5
; then the set of integers that upon
division by 7 yield the remainder 5 is the residue class
Z
5=5+7
·
Z
=
{ ...,−
9
, −
2
,
5
,
12
,
19
,
26
,
33
,...}.
Two residue classes modulo a fixed number
m
are either the same or disjoint.
2
Therefore, a residue class can be uniquely identified by any of its elements. Thus
the elements of a residue class are called
representatives
, and any element can
serve as representative of the class. Equality of residue classes is thus equivalent to
the congruence of their representatives with respect to the given modulus. Since
upon division with remainder the remainder is always smaller than the divisor,
for any integer
m
there can exist only finitely many residue classes modulo
m
.
Now we come to the reason for this extensive discussion: Residue classes
are objects with which one can do arithmetic, and in fact, by employing their
representatives. Calculating with residue classes has great significance for algebra
and number theory and thus for coding theory and modern cryptography. In what
follows we shall attempt to clarify the algebraic aspects of modular
a
rithmetic.
Let
a
,
b
,and
m
be integers,
m>
0
. For residue classes
a
and
b
modulo
m
we define the relations “
+
”and“
·
”, which we call addition and multiplication
(of residue classes), since they are based on the like-named operations on the
integers:
a
+
b
:=
a
+
b
(the sum of classes is equal to the class of the sum)
;
a · b
:=
a · b
(the product of classes is equal to the class of the product)
.
2
Two sets are said to be
disjoint
if they have no elements in common, or put another way, if
their intersection is the empty set.