Biomedical Engineering Reference
In-Depth Information
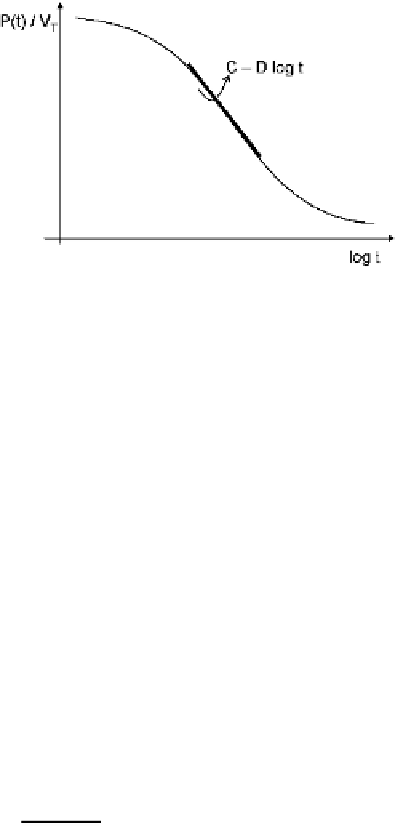
Fig. 1.1
Schematic
representation of the
quasi-linear dependence of
the pressure-volume ratio
with the logarithm of time
means of exponential functions suggested a new interpretation of mechanical prop-
erties in lungs [
134
]. In their endeavor to obtain a relation for compliance which
would be independent on the size of the lungs, they concluded that the pressure-
volume curve is a good tool in characterizing viscoelasticity. Shortly afterwards,
Hildebrandt used similar concepts to assess the viscoelastic properties of a rubber
balloon [
61
] as a model of the lungs. He obtained similar static pressure-volume
curves by stepwise inflation in steps of 10 ml (volume) increments in a one minute
time interval. He then points out that the curves can be represented by means of a
power-law function (see Fig.
1.1
).
Instead of deriving the compliance from the PV curve, Hildebrandt suggests to
apply sinusoidal inputs instead of steps and he obtains the frequency response of
the rubber balloon. The author considers the variation of pressure over total volume
displacement also as an exponentially decaying function:
P(t)
V
T
P(t)
V
T
=
At
−
n
+
B,
=
C
−
D
log
(t)
(1.1)
with
A
,
B
,
C
,
D
arbitrary constants,
V
T
the total volume,
t
the time, and
n
the
power-law constant. The transfer function obtained by applying Laplace to this
stress relaxation curve is given by
P(s)
V
T
A
(
1
−
n)
B
s
=
+
(1.2)
s
1
−
n
with
the Gamma function. If the input is a step
v(t)
=
V
T
u(t)
, then
V(s)
=
V
T
/s
and the output is given by
P(s)
T(s)V
T
/s
with
T(s)
the unknown transfer func-
tion. Introducing this into (
1.2
) one obtains
=
P(s)
V(s)
=
As
n
(
1
T(s)
=
−
n)
+
B
(1.3)
By taking into account the mass of air introduced into the balloon, an extra term
appears in the transfer function equation:
P(s)
V(s)
=
As
n
(
1
L
r
s
2
=
−
+
+
T(s)
n)
B
(1.4)
with
L
r
the inductance. The equivalent form in frequency domain is given by