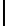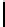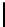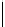Cryptography Reference
In-Depth Information
×
0
1
α
α
2
0
0
0
0
0
α
2
1
0
1
α
α
2
α
3
=1
α
0
α
α
2
α
2
α
3
=1
α
4
=
α
0
Table 4.8 -
Multiplication in field
F
4
.
m
=log
2
(
q
)
,having
β
as a root. This polynomial is unique and irreducible
in
F
2
.If
β
is a primitive element of Galois field
F
q
then polynomial
m
β
(
x
)
is
exactly of degree
m
. Note that a polynomial with coecients in
F
2
satisfies the
following property:
[
f
(
x
)]
2
p
=
f
(
x
2
p
)
[
f
(
x
)]
2
=
f
(
x
2
)
⇒
So, if
β
is a root of polynomial
f
(
x
)
then
β
2
,β
4
,
are also roots of this poly-
nomial. The minimal polynomial with coecients in
F
2
having
β
as a root can
then be written in the form:
···
m
β
(
x
)=(
x
+
β
)(
x
+
β
2
)(
x
+
β
4
)
···
If
β
is a primitive element of
F
q
, the minimal polynomial with coecients in
F
2
being of degree
m
, it can also be written:
(
x
+
β
2
m−
1
)
m
β
(
x
)=(
x
+
β
)(
x
+
β
2
)(
x
+
β
4
)
···
Example 2
Let us calculate the minimal polynomial associated with the primitive element
α
of Galois field
F
4
.
F
4
:
0
,
1
,α,α
2
The minimal polynomial associated with element
α
therefore has
α
and
α
2
(
m
=2
) as roots, and can be expressed:
m
α
(
x
)=(
x
+
α
)(
x
+
α
2
)=
x
2
+
x
(
α
+
α
2
)+
α
3
Taking into account the fact that
α
3
=1
and that
α
+
α
2
=1
in field
F
4
,the
polynomial
m
α
(
x
)
is thus equal to:
m
α
(
x
)=
x
2
+
x
+1