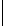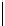Cryptography Reference
In-Depth Information
m
g
(
x
)
Code
CRC-12
12
14017
CRC-16
16
300005
CRC-CCITT
16
210041
CRC-32
32
40460216667
Table 4.3 - generator polynomials of some codes CRC.
The most widely-used CRC codes have the parameters
m
=12
,
16
,
32
and their generator polynomials are given, in octals, in Table 4.3.
Note:
g
(
x
) = 14017
in octals corresponds to 1 100 000 001 111 in
binary, that is:
g
(
x
)=
x
12
+
x
11
+
x
3
+
x
2
+
x
+1
Non-primitive BCH code
The generator polynomial of a non-primitive BCH code (with
l
=1
) correct-
ing at least
t
errors (constructed distance
d
=2
t
+1
)has
2
t
roots of the form:
β, β
2
,β
3
,...,β
2
t
where
β
is a non-primitive element of a Galois field
F
q
.Taking
into account the fact that the minimal polynomials
m
β
j
(
x
)
and
m
β
2
j
(
x
)
have
the same roots, the generator polynomial of a non-primitive BCH code is equal
to:
g
(
x
)=
S.C.M
.
(
m
β
(
x
)
,m
β
3
(
x
)
.....m
β
2
t−
1
(
x
))
We can show that length
n
of the words of a non-primitive BCH code is no
longer of the form
2
m
1
but is equal to
p
,where
p
is the exponent of
β
such
that
β
p
=1
(
p
is the order of
β
). A Galois field
F
q
has non-primitive elements
if
2
m
−
1
is not prime. The non-primitive elements are then of the form
β
=
α
λ
where
λ
is a divisor of
2
m
−
−
1
and
α
is a primitive element of the field.
Example 4.10
Let there be a Galois field
F
q
with
m
=6
and
q
=64
.Thequan ty
2
m
1=63
is not equal to a prime number; it is divisible by 3, 7, 9, 21 and 63.
The non-primitive elements of this field are therefore
α
3
,α
7
,α
9
,α
21
,α
63
=1
.
Let us build, for example, a non-primitive BCH code having an error correction
capability at least equal to
t
=2
on field
F
64
and let us take
β
=
α
3
as the
non-primitive element. We have two minimal polynomials to calculate
m
β
(
x
)
and
m
β
3
(
x
)
. Taking into account the fact that
β
21
=
α
63
=1
, the roots of these
polynomials are:
−
m
β
(
x
)
:roots
β, β
2
,β
4
,β
8
,β
16
,β
32
=
β
11
m
β
3
(
x
)
:roots
β
3
,β
6
,β
12