Environmental Engineering Reference
In-Depth Information
Sect.
4
the numerical method, valid in shallowwater approximation, is presented. The
main results are presented in Sect.
5
, in particular, the emergence of wave breaking,
the behavior of the waves around caustics, the existence of dislocations and the
recovery of a linear behavior far from the caustics. Finally in Sect.
6
the conclusion
are drawn.
2 Spatial Focusing, Caustics and Dislocations
In order to give a picture of the spatial focusing let us consider that surface waves
are produced by a parabolic wave maker. The equation of a parabola is:
ax
0
.
y
0
=
(4)
The first approximation in the study of this wave field is the use of geometrical optics,
that is, it is assumed that rays start in the parabola and move perpendicular to it. The
wave fronts—as shown in Fig.
2
—are obtained by a knowledge of normal vector at
each point of the parabola. As it can be seen, in the vicinity of the parabola the size of
wavefronts decrease as the wave progresses, that implies a growth in the amplitude
because energy must be conserved (the viscosity has been neglected). Locally the
rays form a beam converging in the center of curvature of the parabola. For a point
(
x
0
,
y
0
)
lying in the parabola, the curvature is:
2
a
ʺ
=
4
a
2
x
0
3
/
2
.
(5)
1
+
0.6
0.5
0.4
0.3
0.2
0.1
0
−0.4
−0.2
0
0.2
0.4
X
Fig. 2
Wave fronts produced by a parabolic wave maker. The
black lines
are caustics, which
intersect in a point (Huygens cusp). The caustics can be considered as the locus where the wavefronts
are folded and also as the
curves
where wave amplitude become infinite according to ray theory.
Focusing is evident if we consider that size of wave fronts reduces before the Huygens cusp
























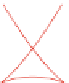









































Search WWH ::

Custom Search