Biomedical Engineering Reference
In-Depth Information
1
− ν
1
2
E
1
1
− ν
2
E
2
1
E
R
=
+
(5-3)
where
i
is the Poisson's ratio and
E
i
is the elastic modulus for each
body, and for which isotropic elasticity has been assumed. (Note the
direct analogy to
Eq. 2-9
in
Chapter 2
of this volume.) In the following
sections we will see how these ideas have influenced modern
nanoindentation testing. To continue with the Hertzian contact theme, we
will start with spherical indentation before moving on to consider flat
punch and conical/pyramidal indentation. As noted in the introduction to
this chapter, the mechanisms for solving elastic contact problems will not
be considered here, only the solutions at textbook-level. In addition to
the texts mentioned earlier,
3,4
the reader is also referred to the classic
work of Sneddon
9
concerning elastic contact.
3.1.
Spherical (Hertzian) elastic contact
R
=
R
i
where
R
i
is the indenter tip radius. The indenter is typically
penetrated only a small fraction of its radius into the material, such that
the projected contact radius (
a
) is much smaller than the indenter radius.
The contact radius can be related to the radius (
R
) and total indentation
depth (
h
) as:
a
=
Rh
(5-4)
The load-displacement (
P
-
h
) relationship for spherical (Hertzian contact)
indentation is:
4
R
E
P
=
)
h
3/2
(5-5)
3
(1
− ν
2
In this case, the indenter has been assumed to be much stiffer than the
sample (
E
s
<<
E
i
) such that the reduced modulus
E
R
is simply the plane
strain modulus for the sample,
E
R
=
E
s
/(1 −
s
2
).
For a perfectly elastic spherical indentation experiment, the load-
mechanism to determine if the contact is perfectly elastic is to estimate
the indentation strain
i
as:

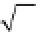


Search WWH ::

Custom Search