Graphics Reference
In-Depth Information
800
8
50
600
6
4
400
2
200
0
0
0
−2
−200
−4
−400
−6
10
−50
−8
−600
−10
5
10
10
−800
5
−10
5
0
2
−12
−5
0
0
1
−5
0
2
−5
−5
0
1
1.5
5
0.5
−1
−0.5
0
−10
−10
−1.5
−1
−10
10
−2
−2
(a)
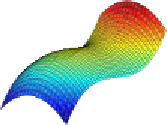
(b)
(c)
Figure 8.1:
(a) e graph of
f.x;y/Dx
2
y
2
. e point
.0;0/
is a non-degenerate critical point.
(b) and (c) e graphs of
f.x;y/Dx
3
3xy
2
(a “monkey saddle”) and
f.x;y/Dx
3
y
2
. In both
cases the point
.0;0/
is a degenerate critical point [
24
].
An important property is that a Morse function defined on a compact manifold admits only
finitely many critical points, each of which is isolated. is means that, for each critical point
p
,
it is always possible to find a neighborhood of
p
not containing other critical points.
8.1.1 INTEGRAL LINES
Given a Riemannian metric on
M
(see [
79
,
80
,
94
] for more details in these concepts) and a
local coordinate system
.x
1
;:::;x
n
/
with orthonormal tangent vectors
@
@x
i
.P/
,
iD1;:::;n
, the
gradient
of a function
f
in a point
P
is the vector:
rf.P/D
@f
@x
i
.P/
T
:
In particular the gradient is the zero vector iff the point
P
is critical.
Definition 8.1
(Integral line)
An
integral line
WR!M
is a maximal path such that:
@
@s
.s/Drf..s//;8s2R:
is means that the velocity vectors along the curve
agree with its gradient. Each integral
line is open at both ends and those points are critical points. Integral lines are pairwise disjoint
and supposing that a critical point is an integral line itself, the integral lines partition
M
.
8.1.2 CONCEPTS IN ACTION
Critical points for shape characterization
Critical points and their configuration give a suitable
framework to formalize and solve several problems related to shape understanding. For example,

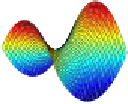
















































Search WWH ::

Custom Search