Graphics Reference
In-Depth Information
6. MAPS AND DISTANCES BETWEEN SPACES
isometries. e experiments in [
128
] show that it can find intrinsic point correspondences in cases
of extreme deformation (Figure
6.6
). e drawbacks are that it can only deal with genus zero sur-
faces, and it may suffer from bad artefacts when the meshes in consideration have “bad” triangles.
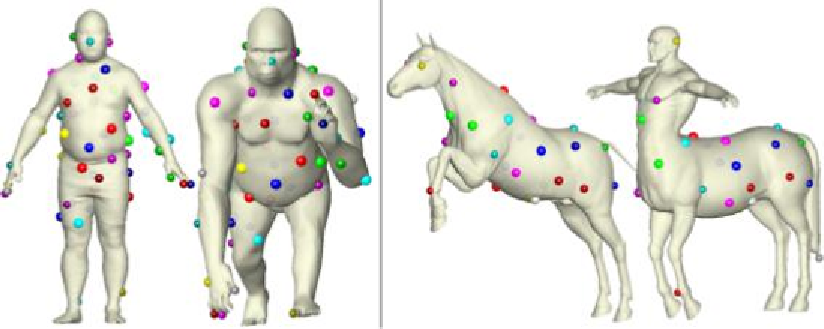
Figure 6.6:
Correspondences between the models of a gorilla and a man (left), and of a centaur and
a horse.
Similar ideas led in [
114
] to an algorithm for detecting intrinsic symmetries on a surface
mesh, a problem which has applications in surface compression, completion, matching, beauti-
fication, alignment. Indeed, looking for intrinsic symmetry transformations means finding iso-
metric transformations that map a surface onto itself (self-isometries), which are contained in a
group of Möbius transformations. Based on these observations, the algorithm 1) generates a set
of symmetric points by detecting critical points of the Average Geodesic Function, 2) enumerates
small subsets of those feature points to generate candidate Möbius transformations, and 3) selects
among those candidate Möbius transformations the one(s) that best map the surface onto itself.
6.2
DISTANCES BETWEEN SPACES
From the problem of comparing subsets of the same metric space (sections
6.2.1
and
6.2.2
) we
move towards the comparison of two metric spaces (i.e., two spaces possibly equipped with dif-
ferent distances, section
6.2.3
) or two topological spaces, section
6.2.4
. First we start to show
how in a metric space
.M;d/
, distances between points can originate distances between subsets.
A first example is the Hausdorff distance, a further example is the
bottleneck
distance, also known
as
matching
or
multiset-multiset
distance.
Search WWH ::

Custom Search