Graphics Reference
In-Depth Information
3. GEOMETRY, TOPOLOGY, AND SHAPE REPRESENTATION
3.4 CONTINUOUS AND SMOOTH FUNCTIONS BETWEEN
TOPOLOGICAL SPACES
e continuity of functions is the building block to reason in terms of
equivalence
between spaces.
We will see in the coming chapters that equivalence between spaces is exploited many times in
shape analysis: shifting the analysis from one space to another, we may simplify our reasoning
thanks to theoretical results that hold in the new space. e important point is to understand
under which conditions we may consider two spaces equivalent: the way to go is continuity and
smoothness.
Let us recall that a function between topological spaces is said to be
continuous
if the inverse
image of every open set in the co-domain space is open in the domain space. is simple and
elegant formulation of continuity may be further strengthened by asking that both the function
and its inverse are continuous: a
homeomorphism
is a bijection that is continuous and whose inverse
is also continuous. From the viewpoint of topology, if there exists a homeomorphism between two
spaces, then the spaces are essentially identical. Figure
3.4
shows examples of homeomorphic and
non homeomorphic spaces.
If we want something more than topological equivalence, we have to introduce another
piece of mathematics, which captures the equivalence between spaces also at differential level.
e reader interested to deepen the concepts listed in the remainder of this chapter can refer to
the topics [
80
,
94
,
149
].
(a)
(b)
(c)
Figure 3.4:
e spaces in (a) and (b) are homeomorphic while the example in (c) is not; indeed,
the third model has a different number of holes and cannot be obtained from the previous ones by
continuous deformations.
Let
X
be an arbitrary subset of
R
n
. en a function
f WX!R
m
is called
smooth
if for
every point
x2X
there is an open set
UR
n
and a function
FWU!R
m
such that
FDf
jX
on
X\U
and
F
has continuous partial derivatives of all orders.
In particular, given
XR
n
and
YR
m
, the smooth function
f WX!Y
is a
diffeomor-
phism
if
f
is bijective and
f
1
WY!X
is also smooth. If such a function exists, the spaces
X
and
Y
are
diffeomorphic
; in this case they are intrinsically equivalent because they may be considered
two copies, with two different coordinate systems, of the same abstract space.
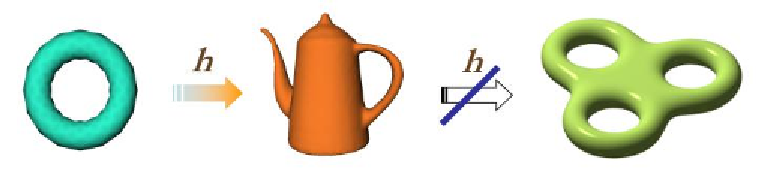
Search WWH ::

Custom Search