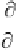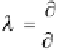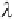Geology Reference
In-Depth Information
constraint associated with the smallest (i.e., most negative)
Lagrange multiplier is removed from the active set, and the
iterative process continues until all Lagrange multipliers are
positive.
The reason that the Lagrange multipliers must be pos-
itive at the optimal solution is as follows. One interpre-
tation of the Lagrange multipliers is the change in the
objective function with a change in the constraint. Using
equation (10.44) and the fact that
A
ij
is simply ∂
g
i
/∂
c
j
for
the constraint
g
i
(
c
) =
A
i
c
−
b
i
, we have
6. If no more inequality constraints have been violated
(or none at all), check
λ
(
k
)
. If any multiplier associated
with any inequality constraint is negative, remove the
constraint. If more than one multiplier is negative, remove
the constraint corresponding to the most negative
k
i
from the active set and go to step 3.
7. The iterative process ends when no more constraints
are violated and all Lagrange multipliers are positive.
At this point the solution is found.
ECICE does not have merit if the number of surfaces is
2 (e.g., sea ice and OW) and the number of observations
is 1 (i.e., the minimum number required). In this case the
optimization approach will produce the same results as
solving the algebraic system equation (10.36) and (10.37).
That is because the inequality constraint will function in
the same way as solution truncation if the concentration
result exceeds 100% or if it drops below 0%. The merit of
the method resides in classifying a number of surface
n
(
n
> 2) with a number of observation ≥ (
n
‐ 1). Even if
n
= 3
and the number of observation is 2 (i.e., the minimum
required), the method will produce better results than
solving the linear equations because the incorporation of
the inequality constraint in the optimization scheme will
provide more rational results than the solution trunca-
tion. The power of the method is revealed when a larger
number of the observations (relative to the given number
of surfaces) is used. A combination of observations from
different sensors such as VIS, TIR, PM, or radar can be
used as input to the algorithm.
As mentioned before, to account for the distribution
of the observation parameters for each surface (instead of
using a single tie point), ECICE uses a large number of
CRVs to retrieve an equally large number of possible solu-
tions of the concentration vector for each footprint obser-
vation (pixel). The number varies typically between 500 and
2000 (user's choice to compromise between accuracy of the
solution and computation time). The CRVs are selected
using the input probability distribution function (pdf) of
the observation parameters. A random number generator is
used for this task. The process of obtaining the CRVs for a
certain parameter using its pdf is illustrated in Figure 10.13.
The figure shows a pdf of a given observation
O
(it can be
brightness temperature, backscatter, albedo, or any param-
eter derived from a satellite measurement) at the top panel
and its cumulative distribution function
F
(
O
) at the bottom
panel. Each generated random number
r
is used as an index
to determine the corresponding CRV as CRV =
F
− 1
(
r
). The
use of the cumulative probability allows the CRVs to mimic
the given pdf of the observation. When two or more of the
used observations are correlated (e.g., backscatter from
HH and VV polarizations), the same random number is
used to generate the CRVs in order to maintain correlation
in the generated CRVs. It should be emphasized that the
input pdf does not have to follow any particular function.
f
c
n
g
c
i
0
(10.53)
i
i
1
j
j
Therefore, by the chain rule of differentiation:
f
g
(10.54)
i
i
Since the inequality constraints are of the form
g
i
(
c
) ≥ 0,
a negative value of
λ
i
implies that an increase in the
constraint value (i.e., movement of the solution into
the feasible region, away from the boundary) will decrease
the value of the objective function. This suggests that
removing the corresponding constraint from the active
set will improve the estimate of the solution. If all
Lagrange multipliers are positive, no improvement in
the objective function is possible, therefore the optimal
solution has been found.
The optimization method is summarized in the
following:
1. Choose an initial feasible solution,
c
(0)
that satisfies
the equality constraint and all the inequality constraints.
A choice of
c
i
0
02. would be appropriate.
2. Formulate the cost function [equation (10.38)]
and the Lagrange function [equation (10.40)] to include
all the observations and the linear system resulting from
the optimization process [Equation (10.43)]. The latter
includes the equality constraint [Equation (10.37)] as the
only initial active set for the first iteration.
3. Use Newton's method to solve equation (10.39) and
find the intervals from the initial solution that minimizes
the objective function. Then compute
c
(
k
+ 1)
and
λ
(
k
+ 1)
from
equation (10.49).
4. If
c
(
k
+ 1)
=
c
(
k
)
+ Δ
c
(
k
)
violates one or more of the inac-
tive inequality constraints, compute
α
(
k
)
from equation
(10.52). In this case
α
(
k
)
should be less than 1. Otherwise
set
α
(
k
)
= 1, then go to step 6.
5. Update the solution using equation (10.50), then add
the inequality constraint that has just been violated to
the active set by modifying the linear system [equation
(10.43)]. Then go to step 3 for a new iteration.