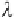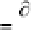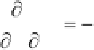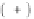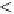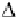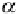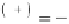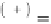Geology Reference
In-Depth Information
derivatives in this system cannot be ill‐conditioned, oth-
erwise, this system becomes numerically difficult to solve.
The first and second derivatives that appear in equa-
tion (10.43) are computed analytically from the objec-
tive function equation (10.40). The first derivatives of
the Lagrange function take the form
The solution is then examined to find if it violates any
of the inequality constraints. If it does not, then that will
be the required solution. In most cases, however, com-
puting the new solution of equation (10.49) will result
in a violation of one or more of the inactive inequality
constraints [equation (10.39)], causing the solution to
become infeasible. To prevent this, a line search tech-
nique is applied so that equation (10.49) becomes:
L
c
f
c
n
A
for
j
1
,
,
n
(10.44)
i
ij
i
1
i
i
k
1
k
k
k
c
c
c
(10.50)
L
(
Ac b
) or
i
1
, ...
l
(10.45)
where
α
(
k
)
is the step length and Δ
c
(
k
)
defines the search
direction. The step length is calculated for each ice type
(or equivalently each inequality constraint)
i
as follows:
i
i
i
where
n
is the number of active constraints. Note that if
all active constraints are satisfied, then equation (10.45)
evaluates to zero. Moreover, the first derivative of the
Lagrange function with respect to concentration is not
exactly the same as the RHS of the linear system, due to
the presence of the Lagrange multiplier terms in equation
(10.44). The reason for this is that the multipliers have
been absorbed into the
λ
new
term in equation (10.43). In
the original Taylor expansion that produces Newton's
method,
λ
new
=
λ
+ Δ
λ
, where Δ
λ
is a step from the current
Lagrange multiplier estimate
λ
. The ECICE algorithm
constructs the linear system [equation (10.43)] by moving
the summation
k
c
k
1
i
if
c
0
i
k
k
c
(10.51)
i
i
k
1
1
if
0
c
1
i
The largest absolute value of
α
i
is then chosen in order to
ensure that no inequality constraints are violated, and
k
is chosen such that
i
k
k
min
i
1
,
,
n
(10.52)
i
n
1
to the LHS and combining it
with the Lagrange multiplier step Δ
λ
.
The second derivatives of the Lagrange function are
obtained as follows:
i
ij
i
If
α
is less than 1, this means that one or more compo-
nents of
c
(
k
+1)
are negative (i.e., violates one or more
of the inequality constraints). For example, if
c
i
k
0.
in the
k th
iteration, and Newton's method produces
c
i
k
0. , this means that
c
i
k
1
0. [according to
[equation (10.49)]. This solution represents a violation of
the inequality constraint
c
i
≥ 0. In this case the value of
α
i
as determined from equation (10.51), is 0.2/0.3 = 0.6667,
i.e., less than 1. If, for example, the solution
c
i
k
1
after
iteration
k
is found to be located at the boundary, i.e.,
c
i
k
1
0, then
c
i
k
must be equal to
c
i
k
and accord-
ingly
α
i
= 1.0. On the other hand, any solution that satis-
fies all inequality constraints will have
α
i
that corresponds
to that constraint equal to 1. So, if
α
is less than 1, the
increment vector Δ
c
should be multiplied by
α
. This is
equivalent to shifting the solution to have it located on the
boundary of the inequality constraint
i
that corresponds
to the minimum of |
α
i
|. The constraint is then added to the
active set. A new linear system is constructed and Newton's
method is applied for a next iteration. This process is
repeated until no new constraints are activated.
Once this is done, the Lagrange multipliers correspond-
ing to the inequality constraints are examined to see if
the active set is correct. If the current solution
c
is indeed
the optimal solution, all Lagrange multipliers of the active
inequality constraints will be positive. If any is negative, the
2
f
cc
c
L
cc
2
ij
,
1
,
,
n
(10.46)
i
j
i
j
2
L
c
Ai
,
j
1
,
,
n
(10.47)
ij
i
j
2
L
0
ij
,
1
,
,
n
(10.48)
i
j
The search for the optimum solution that minimizes
equation (10.38) starts with an initial solution that
satisfies the equality constraint equation (10.37). It then
implements the first iteration by finding the solution that
minimizes equation (10.40) with the equality constraint
as the only active constraint (i.e.,
λ
= 0). This is achieved
by solving the linear system [equation (10.43)]. The solu-
tion is an increment that should be added to update the
initial solution:
k
1
k
k
k
1
k
c
c
c
and
new
(10.49)