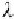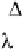Geology Reference
In-Depth Information
of observations must be equal or higher than the num-
ber of ice types (i.e., not including OW). The reason is
explained later.
In addition to these equations the formulation includes
an equality constraint; the summation of concentrations
of each ice type and OW
c
i
must equal 1:
is the corresponding Lagrange multiplier, and
n
is the
total number of active constraints, which is determined
during the optimization process. Minimizing the Lagrange
function [equation (10.40)] is equivalent to minimizing
the objective function [equation (10.38)] subject to both
the equality and inequality constraints, provided that the
correct set of active constraints is found. The concept of
active constraint is introduced in the following.
Equality constraints are always active because feasible
solution points include those that fall on the boundary
formed by the constraint. An inequality constraint, on
the other hand, may or may not be active. It is said to be
active at a feasible point if that point lies on the boundary
of the feasible domain of the solution. This condition
will arise if the solution that minimizes the cost function
is found to be violating the constraint. In this case, the
solution is forced to be relocated to the boundary of the
constraint (as will be further explained later). When an
inequality constraint becomes active, it will take the form
of an equality constraint because the feasible solution is
now located on the boundary of the inequality constraint
c
k
= 0 (
i
= 1, 2, …,
n
).
in
c
1
(10.37)
i
1
The ice concentration vector (
c
) is the solution that mini-
mizes the following cost function. The elements of (
c
) are
the partial concentration of each surface (i.e., requested
ice types plus OW):
2
2
m
n
in
f
()
c
cTRN
/
c
i
1
(10.38)
iij
,
o j
,
j
j
1
i
1
i
1
where
R
o
,
j
is the radiometric observation
j
,
m
is the num-
ber of observations,
N
j
is a normalization factor that is
introduced to ensure that the error terms in equation
(10.38) have the same order of magnitude. The factor is
the average of the observation
j
from all surfaces, i.e.,
⟨
T
i
,
j
⟩ for all
i
. In other words, the normalization factor for
each radiometric parameter should account for values of
the parameter from all surfaces. Equation (10.37) appears
in the cost function since its exclusion would cause the
matrix of the second derivatives of the function to be
ill‐conditioned or singular, making the problem difficult
to solve (this matrix is needed to find the minimum of
the cost function).
In order to avoid a solution for ice concentrations
outside the feasible domain, the formulation includes
the following inequality constraint:
c
k
0 ,, ,
i
n
(10.41)
The coefficients for the equality constraints in equation
(10.40) are
A
i
= [1, 1, 1, 1] and
b
i
= 1. If an inequality con-
straint
k
has become active (e.g.,
c
k
= 0), then
A
i
= 0 for all
i
except for the component
k
, while
b
i
= 0 for all
i
. For
example, if
c
2
becomes active (
c
2
= 0), then
A
i
= [0, 1, 0, 0]
and
b
i
= 0. Note that not all inequality constraints will be
active at the same time.
The algorithm uses Newton's method to find the solu-
tion that minimizes the Lagrange function equation
(10.40). The solution is obtained by taking a second‐
order Taylor expansion of the function around an initial
feasible point and set the first derivative to zero:
0
££
c
i
100
(10.39)
In unconstrained optimization, the necessary and suf-
ficient conditions for a minimum are defined by setting
the first derivative of the objective function to zero while
the second derivative should be greater than zero. In the
case of multivariable problems, the gradient vector is
zero and the eigenvalues of the matrix of second deriva-
tives must all be greater than zero. On the other hand, in
an unconstrained optimization problem the notion of
Lagrange function
L
is introduced [
Fletcher
, 1987]:
c
Lc
,
0
where
(10.42)
The parameter
λ
is the set of Lagrange multipliers that
satisfies the solution. The result is the following system
of linear equations:
2
T
c
f
f A
A
(10.43)
0
0
new
n
L
(
c
,
)
f
()
c
(
Ab
c
)
(10.40)
i
i
i
In this system,
A
is the matrix formed by taking each
A
i
as a row. Solving this system yields a step Δ
c
toward the
solution and a new estimate of the Lagrange multipli-
ers
λ
new
. As mentioned previously, the matrix of second
i
1
Here, (
A
i
c
−
b
i
) is an active constraint, rewritten in vector
form, which originates from the inequality constraint
i
,
λ
i