Global Positioning System Reference
In-Depth Information
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
36, are significant for satellite orbital computations. The higher the altitude of the
satellite, the less the impact of higher-order coefficients on orbital disturbances. A
set of spherical harmonic coefficients can be found in GSFC (2002).
The largest coefficient in (3.71) is
C
20
. This coefficient represents the effect of the
flattening of the earth on the gravitational field. Its magnitude is about 1000 times
larger than any of the other spherical harmonic coefficients.
Useful insight into the orbital disturbance of the flattening of the earth is obtained
by considering the effect
C
20
only. An analytical expression is obtained if one ex-
presses the equations of motion (3.68) and (3.69) in terms of Kepler elements. The
actual derivation of such equations is beyond the scope of this topic. The reader is
referred to Kaula (1966). Mueller (1964) offers the following result,
a
3
1
/
2
a
e
2
2
J
2
1
1
.
5 sin
2
i
3
[68
cos
2
i
ω =−
a
1
e
2
+
−
(3.75)
−
a
3
1
/
2
a
e
2
Lin
—
1
——
Nor
PgE
3
2
J
2
cos
i
Ω =−
a
1
e
2
(3.76)
−
J
2
√
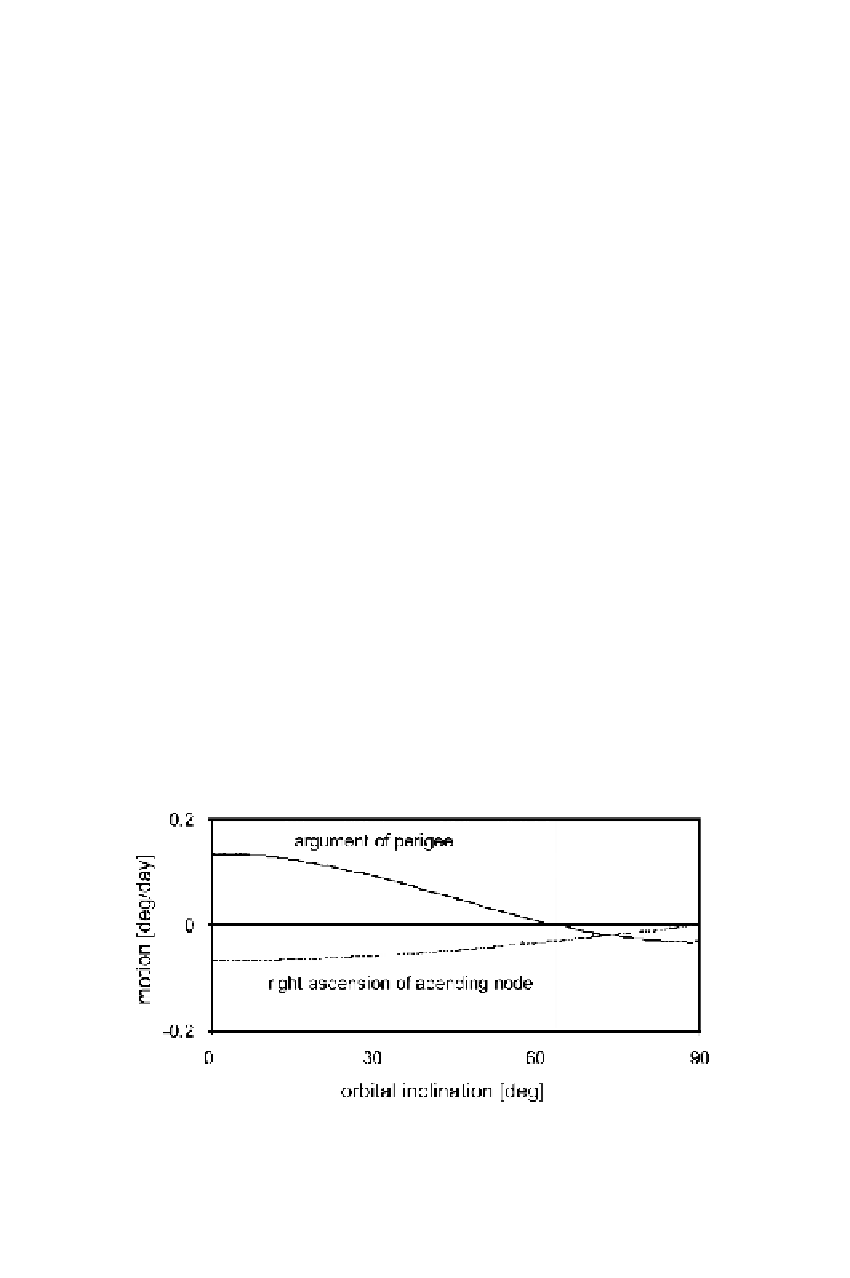
5. The variations of
th
e argument of perigee and the right ascension of the ascending node are shown in
Fi
gure 3.4 as a function of the inclination. At the critical inclination of approximately
63
.5° the perigee motion is stationary. The perigee and the node regress if
i>
63
.
5°.
Th
is orbital plane rotation is zero for polar orbits
i
C
20
In
these equations we have made the substitution
=−
90°. Equation (3.76) is also
us
eful for understanding the connection between the earth flattening and precession
an
d the 18.6-year nutation/tidal period.
=
[68
Figure 3.4 Impact of the earth's flattening on the motion of the perigee and the nodal
lin
e.
The data refer to
a
=
26,600 km.