Cryptography Reference
In-Depth Information
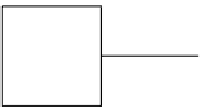
MAC
c
i
M
i
Adversary
(
M
,
c
)
Figure 3.12.
Adversarial model for message authentication codes.
cannot suspect them for having been sent to the recipient by an adversary since it must
have been generated by the legitimate user. An adversary may however try to swap,
erase, or replay some MAC-ed messages in a communication session. This is typically
thwarted by adding a sequence number within the message, as it will be illustrated in
Chapter 12.
3.4.3 MAC from Block Ciphers: CBC-MAC
A famous construction for MAC is the CBC-MAC construction. A first idea for this
construction is to take the last encrypted block of the CBC encryption of the message
asaMAC.
This idea is however not secure. Let us assume that we know three pairs (
M
1
,
c
1
),
(
M
2
,
c
3
) such that
M
1
and
M
3
have the same length and
M
2
is the concatenation
of
M
1
and another message. Let us denote
M
2
=
c
2
), (
M
3
,
M
2
where
B
is a single
message block. If
C
denotes the block cipher (with an unknown key), the encrypted
block of
M
2
which matches
B
is
M
1
||
B
||
C
(
B
⊕
c
1
)
.
We define
B
=
B
||
M
2
. The encrypted block of
M
4
which
B
⊕
c
1
⊕
c
3
and
M
4
=
M
3
||
matches
B
is
C
(
B
⊕
c
3
)
=
C
(
B
⊕
c
1
)
,
which is the same encrypted block as that of
M
2
. Therefore, all encrypted blocks for
M
4
after
B
will be equal to the encrypted blocks for
M
2
after
B
. Hence the last encrypted
block of
M
2
is equal to the last encrypted block of
M
4
, which means that the MAC of
M
4
is
c
2
. We can thus forge a new valid pair (
M
4
,
c
2
).
Following a second idea called “Encrypted MAC (EMAC),” one can encrypt the
last encrypted block of the CBC encryption with another key. We still have an attack
which uses the birthday paradox. If the opponent gets
θ
√
N
valid pairs (where
N
is the
number of possible MACs and
θ
is a constant which defines the probability of success




Search WWH ::

Custom Search