Cryptography Reference
In-Depth Information
Adversary
Message
M
M
r
,
s
M
,
r
,
s
M
r
,
s
M
Signature
Verification
k
∈
Z
p
−
1
r
=
g
k
0
≤
r
<
p
y
r
r
s
mod
p
≡
g
H
(
M
)
(
mod
p
)
H
(
M
)
−
xr
s
=
mod
p
−
1
k
Secret key
x
Public key
y
y
AUTHENTICATED
g
x
mod
p
y
=
Generator
Figure 10.5.
ElGamal signature scheme.
Public parameters
: a large prime number
p
, a generator
g
of
Z
p
.
Setup
: generate a random
x
g
x
∈
Z
p
−
1
and compute
y
=
mod
p
.
Secret key
:
K
s
=
x
.
Public key
:
K
p
=
y
.
Message digest
:
h
Z
p
−
1
.
Signature generation
: pick a random
k
=
H
(
M
)
∈
Z
p
−
1
, compute
r
g
k
∈
=
mod
p
and
s
=
h
−
xr
mod
p
−
1, the signature is
σ
=
(
r
,
s
).
k
Verification
: check that
y
r
r
s
g
h
≡
(mod
p
) and 0
≤
r
<
p
.
σ
(See Fig. 10.5.) We first prove that the signatures are correct: if
was correctly com-
puted, we have 0
≤
r
<
p
and
y
r
r
s
g
xr
+
ks
g
h
≡
≡
(mod
p
)
.
Now we can study the security of this scheme: the difficulty to forge valid signatures.
g
h
(mod
p
).
This is quite easy if we know how to compute the discrete logarithm of
y
(which is
actually the secret key). It is quite easy as well, in general, if we forget the requirement
0
A signature forgery consists of finding
r
and
s
such that
y
r
r
s
≡
Z
p
−
1
≤
r
<
p
. Indeed, one can just pick
α
∈
Z
p
−
1
and
β
∈
at random, take
r
p
=
y
α
g
β
mod
p
,
s
=
h
/β
mod (
p
−
1), and
r
p
−
1
=−
s
α
mod (
p
−
1), then reconstruct
r
such that
r
mod
p
=
r
p
and
r
mod (
p
−
1)
=
r
p
−
1
by using the Chinese Remainder
Theorem.
One problem with the plain ElGamal scheme concerns the signature length. As-
suming that
p
is of length 1024 bits, it means that
σ
is of length 2048 bits (256 bytes),
which is quite long.











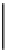







Search WWH ::

Custom Search