Cryptography Reference
In-Depth Information
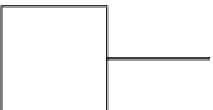
∈
L
2
?
Yes/ No
x
1
,...,
x
q
∈
L
1
?
Yes/ No
w
Figure 8.2.
Oracle turing machine.
can compute the factorization of
n
by using an oracle that implements the Carmichael
function
λ
(
n
).
Two languages are
Turing-equivalent
if they reduce to each other in polynomial
time.
We have to make two important remarks. First of all, the decision problems are
symmetric: if
L
1
reduces to
L
2
, then the complement of
L
1
also reduces to
L
2
(since the
oracle Turing machine is deterministic and the running time is bounded, we just need
to wait until the time bound in order to decide whether or not a given word is in
L
1
).
Second, the oracle solves the decision problem of membership in
L
2
which is believed
to be harder than accepting
L
2
in asymmetric cases such as NP-complete problems. For
instance, the SAT decision problem is at least as hard as accepting co-SAT. Therefore
we can solve both NP (due to the Karp reduction) and co-NP with P
SAT
. For this reason
people believe that NP is not closed under the Turing reduction. Hence we should limit
ourselves to NP
co-NP as a reference class for intractable problems, which is the
case of cryptography.
∩
8.4
Exercises
}
∗
of all bitstrings with an even number of bits
equal to 1. Prove that it is a regular language by producing a finite automaton which
recognizes L.
Exercise 8.1.
Let L be the subset of
{
0
,
1
Do the same with L equal to the set of all numbers which are congruent to 1 modulo
3 represented in binary notations,
i.e.
L is the set of all bitstrings
(
a
0
,
a
1
,...,
a
n
)
such that
n
a
i
2
i
≡
1
(mod 3)
i
=
0
Let x and y be two integers. Inspiring yourself from the square-and-multiply algorithm
from right to left, do the same with L equal to the set of all bitstrings which represent
a number which is congruent to x modulo y.


Search WWH ::

Custom Search