Information Technology Reference
In-Depth Information
Fig. 3.2
Function
u(x)
and
its piecewise linear
approximation
(
I
N
u)(x)
where the load vector
l
is given by
M
φ
−
l
(t)
=
f
(t)
−
A
φ
,
2
denoting the coefficient vector of
φ
.For
Neumann boundary conditions, i.e.
∂
x
u(t, a)
(φ
1
(t),
0
,...,
0
,φ
2
(t))
∈ R
N
+
with
φ
=
=
φ
1
(t)
,
∂
x
u(t, b)
=
φ
2
(t)
, the bound-
ary degrees of freedom must be kept.
3.4.2 Initial Data
H
1
(G)
(e.g.
u
0
being the payoff of a put or call option), we can use
nodal interpolation
,i.e.
u
N,
0
=
I
N
u
0
.For
u
∈
H
1
(G)
, define the nodal interpolant
In the discretization (
3.14
), we need an approximation of
u
0
in
V
N
.If
u
0
∈
I
N
u
∈
S
1
by
T
N
+
1
(
I
N
u)(x)
:=
u(x
i
)b
i
(x),
(3.24)
i
=
0
as illustrated in Fig.
3.2
. Since
b
i
(x
j
)
=
δ
ij
, we get
(
I
N
u)(x
i
)
=
u(x
i
)
.
For
u
H
1
(G)
, the nodal value
u(x
i
)
is well defined due to Theorem
3.1.4
.
∈
H
1
(G)
S
1
T
Lemma 3.4.2
The interpolation operator
defined in
(
3.24
)
is
bounded
,
i
.
e
.
there exists a constant C
(
which is independent of N
)
such that
I
N
:
→
H
1
(G).
I
N
u
H
1
(G)
≤
C
u
H
1
(G)
,
∀
u
∈
(3.25)
L
2
(G)
(e.g.
u
0
being the payoff of a digital option), we
cannot use interpolation, but need the
L
2
-projection of
u
0
on
V
N
,i.e.
u
N,
0
=
P
N
u
0
.
For
u
If we only have
u
0
∈
L
2
(G)
,the
L
2
-projection of
u
on
V
N
is defined as the solution of
∈
G
P
N
uv
N
d
x
=
uv
N
d
x,
∀
v
N
∈
V
N
.
(3.26)
G
Using the basis
b
i
,
i
=
0
,...,N
+
1, of
V
N
we can obtain the coefficient vector
u
N
of
P
N
u
0
as the solution of the linear system
M
u
N
=
f
,
with
f
i
=
ub
i
d
x,
i
=
0
,...,N
+
1
.
G














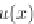

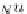




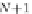



Search WWH ::

Custom Search