Information Technology Reference
In-Depth Information
Fig. 3.1
Reference element
shape functions on the
reference element
K
Furthermore, for
i, j
=
1
,
2 there holds
a
l
(N
j
K
l
,N
i
K
l
)
(
A
l
)
ij
=
α(x)∂
x
N
j
K
l
N
i
K
l
d
x
β(x)∂
x
N
j
γ(x)N
j
K
l
∂
x
N
i
K
l
+
K
l
N
i
K
l
+
=
K
l
h
l
2
α
K
l
(ξ )
4
h
l
N
j
N
i
+
β
K
l
(ξ )
2
h
l
N
j
N
i
+
γ
K
l
(ξ )N
j
N
i
=
d
ξ,
K
where
α
F
K
l
(ξ )
,
β
F
K
j
(ξ )
,
γ
F
K
l
(ξ )
.
β
K
l
(ξ )
α
K
l
(ξ )
:=
:=
γ
K
l
(ξ )
:=
For later purpose, it is useful to split the integral into three parts
(
A
l
)
ij
=
(
S
l
)
ij
+
(
B
l
)
ij
+
(
M
l
)
ij
,
(3.22)
where
2
h
l
K
α
K
l
N
j
N
i
d
ξ,
K
β
K
l
N
j
N
i
d
ξ,
(
S
l
)
ij
=
(
B
l
)
ij
=
h
l
2
γ
K
l
N
j
N
i
d
ξ.
(
M
l
)
ij
=
K
For general coefficients
α(x)
,
β(x)
and
γ(x)
, these integrals cannot be computed
exactly. Hence, they have to be approximated by a numerical quadrature
1
p
w
(p)
j
f(ξ
(p)
j
f(ξ)
d
ξ
≈
),
−
1
j
=
1
using a
p
-point quadrature rule with quadrature weights
w
(p)
j
and quadrature points
ξ
(p)
j
1
,...,p
.
It remains to construct the stiffness matrix
A
. The idea is to express the global ba-
sis functions
b
i
(x)
in terms of the local shape functions. We have for
i
∈
(
−
1
,
1
)
,
j
=
=
1
,...,N
,
N
K
i
+
N
K
i
+
1
,
0
(x)
N
K
1
,
N
+
1
(x)
N
K
N
+
1
.
=
=
=
b
i
(x)












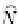

















Search WWH ::

Custom Search