Information Technology Reference
In-Depth Information
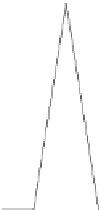
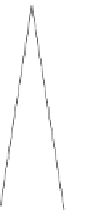
Fig. 2.2
Basis functions
b
i
(x)
,
i
=
1
,...,N
N
×
N
N
With matrices
M
,
A
∈ R
and vector
f
(t)
∈ R
given by
b
b
b
j
(x)b
i
(x)
d
x,
M
ij
:=
b
j
(x)b
i
(x)
d
x,
A
ij
:=
a
a
b
f
i
(t)
:=
f(t,x)b
i
(x)
d
x,
a
we obtain the weak semi-discretization (
2.23
)in
matrix form
:
Find
u
N
∈
C
1
(J
; R
N
),
such that for
t
∈
J
M
u
N
(t)
˙
+
A
u
N
(t)
=
f
(t),
(2.24)
u
0
,
where
u
0
denotes the coefficient vector of
u
N,
0
=
i
=
1
u
0
,i
b
i
.
For the basis functions
b
i
of
V
N
=
u
N
(
0
)
=
span
{
b
i
(x)
:
i
=
1
,...,N
}
, we take the so-
called
hat functions
h
−
1
b
i
:[
a,b
]→R
≥
0
,
i
(x)
=
max
{
0
,
1
−
|
x
−
x
i
|}
,i
=
1
,...,N,
as illustrated in Fig.
2.2
.
For equidistant mesh points
x
i
,
i
=
1
,...,N
with mesh width
h
as in (
2.5
),
x
i
=
a
+
ih, i
=
0
,
1
,...,N
+
1
,h
:=
(b
−
a)/(N
+
1
)
=
x,
N
×
N
sym
we obtain the matrices,
M
,
A
∈ R
, given by
⎛
⎞
⎛
⎞
−
41
2
1
⎝
⎠
⎝
⎠
.
.
.
.
.
.
.
.
.
.
.
.
h
6
1
h
1
−
1
M
=
,
A
=
.
(2.25)
.
.
.
.
.
.
1
14
.
.
.
.
.
.
−
1
−
12


























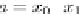
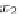




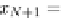







Search WWH ::

Custom Search