Information Technology Reference
In-Depth Information
Fig. 12.2
First compression: a matrix entry
A
(
,k
),(,k)
is set to 0 if
δ
is large enough (
top
).
Second compression: a matrix entry
A
(
,k
),(,k)
issetto0if
δ
sing
is large enough (
bottom
)
Example 12.2.3
Let
a
=
a
=
7. The correspond-
ing compression scheme is plotted in Fig.
12.3
. Zero entries due to the first com-
pression are left white, zero entries due to the second compression are colored red
and non-zero entries blue regardless of their size. Additionally, we plot the number
of non-zero entries which grow like
1,
p
=
2,
p
=
4,
α
=
0
.
5 and
L
=
O
(N)
.For
L
=
7 there are only 14 % non-zero
entries.
The matrix compression induces instead of (
12.6
) a perturbed semi-discretization
u
L
∈
H
1
(J
;
V
L
)
such that
Find
(∂
t
u
L
,v
L
)
+
a(
u
L
,v
L
)
=
0
,
∀
v
L
∈
V
L
,
a.e. in
J,
(12.8)
u
L
(
0
)
=
u
L,
0
.
We have the following analog to Theorem
12.2.1
which states that the convergence
rate of the numerical solutions obtained from space semi-discretization with matrix
compression do not deteriorate.
Theorem 12.2.4
Assume the Lévy density k satisfies Assumption
10.2.3
and
(
12.7
).
Moreover
,
let ε
=
a
−
2
(p
+
α/
2
)
+
a
−
(p
+
α)
be sufficiently small
.
Then
,
for t>
0,
we
have the following a priori error estimate for the perturbed semi-discrete problem
(
12.8
):
p
α
1
,h
p
t
−
u(t)
−
u
h
(t)
L
2
(G)
≤
C
min
{
}
,
where C>
0
is a constant independent of h and t
,
and u is the solution of
(
12.5
).
This can be proven combining the arguments given in [51, Theorem 10.1] and
[123, Theorem 2].

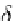








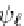














Search WWH ::

Custom Search