Information Technology Reference
In-Depth Information
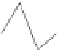
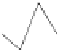
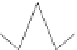
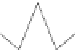
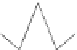
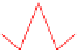
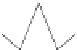
Fig. 12.1
Single-scale space
V
L
and its decomposition into
multiscale wavelet spaces
W
for
L
=
3
(ii) Iterative solution and judicious preconditioning of the linear systems in each
time step,
(iii)
Wavelet finite element bases
for the
preconditioning
and the
matrix compres-
sion
of the nonlocal operators arising with jump type price processes.
We start with explaining spline wavelets on an interval.
12.1 Spline Wavelets
As in Sect. 3.3, we discretize the domain
G
=
(a, b)
by equidistant mesh points
=
···
<x
N
L
+
1
=
a
x
0
<x
1
<x
2
<
b,
2
L
+
1
where we assume the number
N
L
satisfies
N
L
=
−
1 with
L
∈ N
0
and use the
V
N
L
. Then, we have the nested spaces with 2
,
4
,...,
2
L
+
1
notation
V
L
=
subinter-
vals
V
0
⊂
V
1
⊂···⊂
V
L
,
2
+
1
and dim
V
=
−
1
=:
N
. In Sect. 3.3, we generated
V
by a
single-scale
basis
V
=
. Here, we change notation and we write
b
,j
instead of
b
j
to indicate the refinement level. Wavelets constitute a so-
called
hierarchical
or
multi-scale
basis. We start with
span
{
b
,j
(x)
:
1
≤
j
≤
N
}
{
ψ
0
,
1
}
for the space
V
0
.
Then, we add basis functions
{
ψ
1
,
1
,ψ
1
,
2
}
such that span
{
ψ
0
,
1
,ψ
1
,
1
,ψ
1
,
2
}=
{
ψ
2
,
1
,ψ
2
,
2
,ψ
2
,
3
,ψ
2
,
4
}
V
1
. Similarly, we add again basis functions
such that
span
V
2
, and so on. Therefore, we in-
troduce for
∈ N
0
the complement spaces
W
=
{
ψ
0
,
1
,ψ
1
,
1
,ψ
1
,
2
,ψ
2
,
1
,ψ
2
,
1
,ψ
2
,
3
,ψ
2
,
4
}=
span
{
ψ
,k
:
k
∈∇
}
where
1
,...,
2
∇
:= {
}
such that
V
=
V
−
1
⊕
W
,
≥
1 and
V
0
=
W
0
. This decom-
position is illustrated in Fig.
12.1
.
We assume that the wavelets
ψ
,k
have compact support
C
2
−
,
|
supp
ψ
,k
|≤
are normalized in
L
2
(G)
,i.e.
ψ
,k
L
2
=
1, and
Φ
:= {
b
,j
(x)
:
1
≤
j
≤
N
}
has
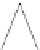

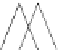
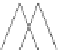
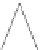
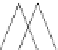
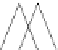

























Search WWH ::

Custom Search