Geology Reference
In-Depth Information
U(x,s) = F(s)(-1/c
2
)(c/s) (x-x*) sinh {(s/c)(x-x*)}
+ U
x
(0,s)(c/s) sinh {(s/c)x} (1.162)
Now, since u(L,t) = 0, it follows from taking time transforms that U(L,s) = 0;
and because L > x*, we obtain
0 = F(s)(-1/c
2
)(c/s) sinh {(s/c)(L-x*)} + U
x
(0,s)(c/s) sinh {(s/c)L} (1.163)
or
U
x
(0,s) = F(s)(1/c
2
) sinh {(s/c)(L-x*)}/{sinh {(s/c)L}}
(1.164)
Back substitution into Equation 1.162 completely determines the transform
U(x,s) as
U(x,s) = F(s)(-1/c
2
)(c/s) (x-x*) sinh {(s/c)(x-x*)} (1.165)
+F(s)(1/c
2
) sinh {(s/c)(L-x*)}(c/s) sinh {(s/c)x}/{sinh {(s/c)L}}
Thus, the timewise solution u(x,t) is in principle known for any excitation
f(t). The required inversion, not performed here, leads to complicated infinite
series solutions in the sine eigenfunction used earlier. Because damping was
ignored, the effects of each movement f(t) remains in our solution for all time.
1.8.2 Example 1-16. Finite string excited by a time-varying point
dipole (i.e., a force couple).
For simplicity, we solve Equation 1.166 subject to the initial flat elevation
u(x,0) = 0 and the static condition u(x,0)/ t = 0 in 0 < x < L. The string is
rigidly pinned at the two end points, with u(0,t) = 0 and u(L,t) = 0.
2
u/ t
2
- c
2
2
u/ x
2
= f(t) '(x-x*)
(1.166)
As before, we take Laplace transforms in time. Following exactly the same
steps, we now obtain the differential equation
s
2
U(x,s) - c
2
U"(x,s) = F(s) '(x-x*)
(1.167)
where we have simplified intermediate results using initial conditions. Notice,
though, that Equation 1.167 contains '(x-x*) and not (x-x*). In order to apply
Laplace transforms in the x direction, we use Equation 1.152 in the form
e
- x
'(x-x*) dx = e
- x*
, where > 0
(1.168)
This leads to s
2
U
( ,s) - c
2
{
2
U
( ,s) - U(0,s) -U
x
(0,s)}= F(s) e
- x*
, and the
only difference from Example 1.15 is the extra factor appearing on the right.
The inversion procedure continues in the same manner.










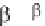
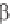
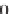




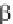








Search WWH ::

Custom Search